SEO-Константа
Яндекс.Директ + оптимизация
Сейчас мы выполним переход от классического поведенческого алгоритма BrowseRank к BrowseRank Plus. Фреймворк так же может помочь в разработке новых алгоритмов. В частности, зависимость продолжительности визитов от нескольких состояний можно использовать для решения проблем, с которыми не способны справиться современные алгоритмы. Приведём расширение алгоритма BrowseRank до BrowseRank Plus в качестве примера разработки расчётного метода в рамках фреймворка.
Спам по-прежнему распространяется в Интернете, поэтому необходимо принимать соответствующие меры по противодействию ему при расчёте важности веб-страниц, в особенности для алгоритмов BrowseRank-типа, которые основаны на графе сёрфинга пользователей. Как описывалось в предыдущей части работы, BrowseRank строит модель непрерывного процесса Маркова на графе сёрфинга пользователя. Главной проблемой BrowseRank является кликовое мошенничество, так как BrowseRank полностью доверяет данным о поведении пользователей и рассчитывает на их основе среднюю продолжительность визита. Это даёт спамерам пространство для манёвра, позволяя совершать мошеннические клики вручную или в автоматическом режиме с целью повышения авторитетности собственных сайтов. В результате будет наблюдаться крупный объём переходов с этих веб-сайтов на спамерские ресурсы. Непосредственное применение BrowseRank в данном случае сгенерирует серьёзное смещение в сторону спама при расчёте авторитетности веб-страниц.
Для решения этой проблемы мы будем по-разному взвешивать переходы с различных веб-сайтов. Если крупная доля переходов была произведена с конкретного веб-сайта, мы можем понизить вес каждого из этих переходов, чтобы пессимизировать влияние кликового мошенничества. Однако в таком случае непрерывный процесс Маркова будет работать не очень хорошо, так как он не распознаёт с каких веб-сайтов производились переходы. Поэтому необходимо разработать новую модель ССПМ, которая будет способна справиться с поставленной задачей. Мы назвали новую модель ССПМ Зеркальным Полумарковским Процессом (ЗПМП), а новый алгоритм, работающий с этой моделью — BrowseRank Plus. Главным преимуществом BrowseRank Plus является его способность противодействовать кликовому мошенничеству, чего не может добиться BrowseRank. Отметим, что идея обобщения BrowseRank до BrowseRank Plus в некотором роде похожа на SimRank (Jeh и Widom, 2002).
Для подробного объяснения алгоритма BrowseRank Plus, опишем ЗПМП и покажем его применение в расчёте авторитетности веб-страницы.
ЗПМП — это новый стохастический процесс, который может использоваться как в информационном поиске, так и в прочих областях.
Определение 4. Сетевой Скелетный Процесса Маркова Z = (X, Y) называется Зеркальным Полумарковским Процессом (ЗПМП), если Yn зависит только от Xn, а Xn-1 и распределения Yn независимы от n. Конкретнее, ССПМ Z = (X, Y) является ЗПМП, если P(Y0≤t|{Xk}k≥0) = P(Y0≤t|{X0}), а P(Yn≤t|{Xk}k≥0) = P(Yn≤t|Xn,Xn-1}) = P(Y1≤t|{X1,X0}) для всех n≥1.
Очевидно, что ЗПМП является частным случаем ССПМ. Более того, ЗПМП схож с Полумарковским процессом (см. пример 3 в Части 4). В Полумарковском Процессе Yn зависит от данного состояния Xn и будущего состояния Xn+1, а в ЗПМП Yn зависит от данного состояния Xn и предыдущего состояния Xn-1. Зависимости противоположны, поэтому новая модель называется Зеркальным Полумарковским Процессом.
Пусть X — вложенная цепь Маркова в ЗПМП Z. Предположим, что пространство состояний S конечно и отображает все веб-страницы. Используем обозначение P = (pij)i,j ∈ S для отображения матрицы вероятностей переходов процесса X. Далее предположим, что существует уникальное стационарное распределение процесса X π~, которое рассчитывается степенным методом (Golub и Loan, 1996).
Пусть j является состоянием (j ∈ S), а Tj — продолжительность пребывания в состоянии j. По Определению 4 получим следующую формулу (6):
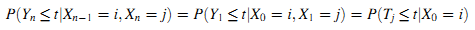
Мы используем iFTj(t) =Δ P(Tj≤t|X0 = i) для определения кумулятивного распределения вероятностей продолжительности пребывания в состоянии j из состояния i. FTj(t) является кумулятивным распределением вероятностей продолжительности пребывания в состоянии j. Получим формулу (7):
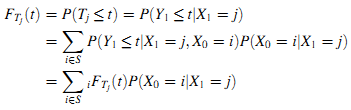
Определение 5. Определим cij =Δ P(X0=i|X1=j) как вероятность вклада (contribution probability) состояния i в состояние j.
Располагая временной однородностью вложенной цепи Маркова X, можно обнаружить, что вероятность вклада cij различается по двум состояниям i и j вне зависимости от времени перехода из i в j.
На основании определения вероятности вклада и кумулятивного распределения вероятностей продолжительности Tj, можно рассчитать среднюю продолжительность пребывания в состоянии j как (8):
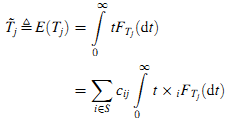
Далее рассчитаем распределение, которое определяется как оценка важности страницы используя стационарное распределение π~ вложенной цепи Маркова X и среднюю продолжительность пребывания Tj~, где α — нормализованный коэффициент для удовлетворения уравнения ∑j ∈S πj = 1. Формула (9):
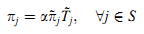
ЗПМП используется нами для расчёта авторитетности веб-страниц. При данном веб-графе и его метаданных, построим ЗПМП модель по графу. Сначала определим стационарное распределение вложенной цепи Маркова X. Затем рассчитаем среднюю продолжительность пребывания с использованием метаданных. Наконец, рассчитаем произведение стационарного распределения вложенной цепи Маркова и средней продолжительности пребывания на страницах — это будет являться авторитетностью страницы. Так как стационарное распределение вложенной цепи Маркова может быть рассчитано степенным методом (Golub и Loan, 1996), сфокусируемся на расчёте времени пребывания.
Предположим, что на страницу j ссылается nj страниц: Ξ j = {ζj1,ζj2, …, ζjnj} (_ S. Фактически вероятность вклада i в j является вероятностью того, что пользователь придёт со страницы i при данном условии перехода на страницу j.
Гипотеза 1. Предположим, что cij — это вероятность вклада i в j, тогда
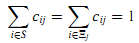
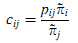
где pij — вероятность перехода с i на j в соответствии с матрицей вероятностей переходов процесса X, а π~ — стационарное распределение процесса x.
Доказательство. Легко получить следующее:
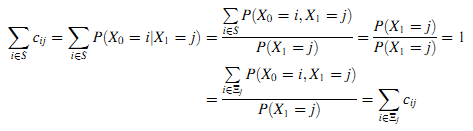
Из-за временной однородности процесса X получим:
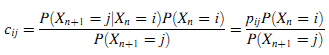
Далее, процесс X имеет стационарное распределение. Если существует его ограничивающее распределение вероятностей, то рассчитаем лимит:
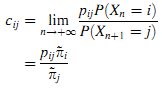
Из (11) легко рассчитать вероятность вклада. Мы используем эвристический метод для этого расчёта.
Предположим, что nj входящих ссылок страницы j расположено на mj вебсайтов, а с вебсайта k (k = 1, …, mj) идёт njk ссылок. Тогда получим (12):
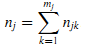
Отметим, что веб-сайт, на котором располагается страница j может существовать в множестве mj веб-сайтов.
Предположим, что mj сайтов, ссылающихся на страницу j это Фj = {фj1, фj2, …, фjmj}. cфjkj — это вероятность того, что пользователь перейдёт на страницу j с сайта фjk, называемая вероятностью вклада сайта.
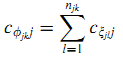
Допустим, вероятность вклада различных страниц одного и того же сайта идентична (14):
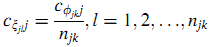
Допустим, что кумулятивные распределения вероятностей с разных веб-страниц одного сайта идентичны. Пусть S~ = {ф1, …, фm} является всеми веб-сайтами, поэтому верно ∀i,k ∈ S, если i,l ∈ фk, k = 1, 2, …, m, (15):
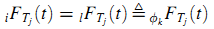
Используем определение фkFTj(t) для отображения кумулятивного распределения вероятностей Tj с вебсайта фk.
Будем считать, что продолжительность пребывания Tj следует экспоненциальному распределению, в котором параметр относится и к странице j и к ссылающемуся вебсайту фk (16):
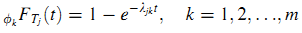
Поэтому продолжительность пребывания зависит от страницы j и ссылающегося веб-сайта, а не ссылающейся страницы.
На основе анализа перепишем (8) в следующем виде (оставив S~ = {ф1, …, фm} выборкой всех сайтов) (17):
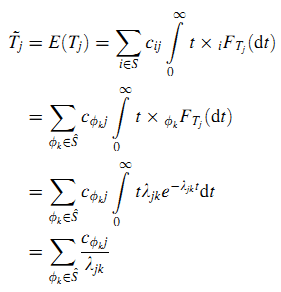
Главной идеей здесь является допущение, что продолжительность визита (полезность) страницы зависит от ссылающегося веб-сайта и расчёт среднего времени пребывания основа на всех сайтов с ссылками. Более того, можно изменить среднюю продолжительность пребывания через изменение двух величин: cфkj и λjk.
Интуитивно, полезность веб-страницы не изменяется в соответствии с предыдущими сайтами, посещёнными пользователем. В случае ссылочного графа если пользователь приходит на данную страницу с веб-сайта с высокой полезностью (авторитетностью, качеством и т.д.), то полезность страницы будет так же высокой. В случае с графом сёрфинга пользователя, если пользователь приходит на данную страницу с сайта с высокой полезностью (популярностью, качеством и т.д.) и следует переходу с высокой частотой, то полезность страницы так же будет высока.
Встаёт вопрос, как рассчитать вероятности вклада от разных сайтов cфkj и оценить параметры разных сайтов λjk. Если имеется достаточно наблюдений визитов, можно оценить параметры λjk, k = 1, …, m. В прочих случаях (недостаточно наблюдений), можно использовать эвристические методы оценки средней продолжительности визита. Для расчёта вероятностей вклада cфkj мы так же можем использовать эвристику.
После введения в ЗПМП мы покажем как сконструирован алгоритм BrowseRank Plus для борьбы с кликовым мошенничеством в расчёте авторитетности страниц. BrowseRank Plus решил эту проблему используя ЗПМП. В данном алгоритме средняя продолжительность визита страницы рассчитывается на основе ссылающихся сайтов. Точнее, образцы записанных продолжительностей различаются в соответствии с различными ссылающимися сайтами через оценку различных параметров λjk, (k = 1, …, m = |S~|). Оценка параметров λjk аналогично методике в BrowseRank. Далее, в BrowseRank Plus вероятность вклада cфkj так же зависит от ссылающихся сайтов. Предположим, что mj сайтов Фj = {фj1, фj2, …, фjmj} ссылаются на страницу j, тогда вероятность вклада определяется как (18):
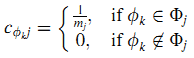
Мы допускаем, что вклады различных ссылающихся сайтов одинаковы. Наконец, средняя продолжительность визита рассчитывается через (17). Поэтому значения на разных сайтах будут отличаться друг от друга.
Главной частью BrowseRank Plus является нормализация веб-сайтов (18). Поясним на примере. Предположим, что существует крупный объём ссылающихся на страницу сайтов в графе сёрфинга пользователя, т.е. сайты, с которых пользователи совершали переход на данную страницу. Кликовое мошенничество обычно характеризуется следующими поведенческими паттернами: а) число кликов высоко и наблюдаемая продолжительность визитов тоже высока (таким образом спамер обманывает алгоритмы BrowseRank-типа чтобы максимизировать эффективность продвижения сайтов). б) переходы совершаются с небольшого количества веб-сайтов (иначе такой способ мошенничества был бы очень затратным). В BrowseRank Plus мы эффективно используем факт б и нормализуем вклады различных сайтов.
Отметим, что это только один простой пример расчёта средней продолжительности визита. Можно разработать и более сложные модификации расчёта. Главной идеей является контролировать вклады с различных сайтов, а ЗПМП предлагает фреймворк для принципиального решения задачи.
Гипотеза 2. Если параметры λjk, k = 1, …, m имеют одинаковое значение, BrowseRank Plus деградирует до BrowseRank.
Доказательство. Если λj1 = λj2 = … λjm =Δ λj, тогда из (17) и (10) получим (19):
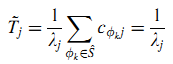
Tj~ является средней продолжительностью визита как в BrowseRank.
Как упоминалось в разделе [Моделирование авторитетности страницы], мы используем произведение стационарного распределения вложенной цепи Маркова X и средней продолжительности пребывания на странице для моделирования важности страницы. Главной причиной для этого является тот факт, что во многих случаях можно доказать, что данное произведение пропорционально ограничивающему распределению вероятностей ЗПМП, если оно существует. Однако его существование возможно только в определённых условиях.
Пусть Tjj — это интервал между двумя успешными переходами из состояния j в ЗПМП. Это значит, что пользователь прошёл цикл из состояния j в состояние j за данный интервал. Все циклы следуют Колебательному Процессу Обновления (Staggered Renewal Process, Papoulis и Pillai, 2001). Пусть E(Tjj) будет средней продолжительностью цикличности состояния j.
Лемма 1. Пусть Z — Зеркальный Полумарковский Процесс. Если матрица вероятностей переходов P вложенной цепи Маркова X минимальна (irreducible), а распределение вероятностей P(Tjj≤t) не является решётчатым (lattice distribution — такое прямое распределение случайной величины, что каждое возможное значение может быть записано в виде a + bn, где a, b не равно 0, а n — целое число). Пусть E(Tjj) < ∞, тогда ограничивающее распределение вероятностей Z существует и применяя Теорему Центрального Предела (Central Limit Theorem), получим (20):
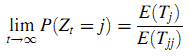
что не зависит от начального состояния i ЗПМП.
Лемма гарантирует существование ограничивающего распределения ЗПМП πj =Δ E(Tj)/E(Tjj).
Теорема 1. Предположим, что ЗПМП определён в конечном пространстве состояний S. Если вложенная цепь Маркова X эргодична, что подразумевает существование и ограничивающей вероятности и стационарного распределения π~ (при этом они идентичны, т.к. lim n → ∞ Pn = 1T π~), а распределения вероятностей P(Tjj≤t) не является решётчатым, а E(Tjj) < ∞, получим (21):
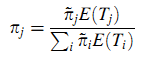
Доказательство. Пусть Tj(k) будет продолжительностью визита k в состояние j, а Nj(n) будет количеством исходов из состояния j за последние n переходов. Пусть pj(n) — это пропорция продолжительности пребывания в состояние j за предыдущие n переходов. В соответствии с леммой получим πj = limn → ∞ pj(n) и по Сильному Закону Больших Чисел (Strong Law of Large Numbers) получим:
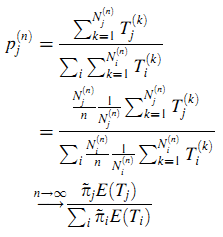
Так же было получено (21).
Сравнивая (9) и (21), можно увидеть, что произведение стационарного распределения вложенной цепи Маркова и средней продолжительности пребывания пропорционального ограничивающему распределению вероятностей ЗПМП.
Предположим, что имеется мобильный граф данных. Мобильный граф содержит веб-страницы, соединённые гиперссылками и предназначенные для доступа с мобильных устройств. Мобильный веб сильно отличается от обычного во многих аспектах. К примеру, топология мобильного графа совершенно не похожа на обычный веб-граф (Jindal и др., 2008), так как владельцы мобильных веб-сайтов стараются создавать больше ссылок на свои собственные страницы или страницы партнёров. Как следствие, наблюдается больше несоединённых компонентов в мобильном графе, а ссылки являются не рекомендацией, а коммерческой связью. В таком случае, оценки алгоритмов типа PageRank не являются адекватными.
Мы предлагаем новый алгоритм под названием MobileRank для расчёта авторитетности веб-страниц в мобильном графе с использованием ЗПМП. Фактически мы рассматриваем новый способ расчёта средней продолжительности визита.
Отметим, что в применении ЗПМП мы допускаем, что продолжительность визита зависит не только от текущей страницы, но и от ссылающегося сайта, то есть ЗПМП способен отображать отношение между сайтами и использовать эту информацию для увеличения или пессимизации полезности страницы. Если ссылка идёт с партнёрского веб-сайта, то применяется пессимизация.
Мы определяем вероятность вклада cфkj так же, как и в BrowseRank Plus (см. (18)). Эвристически рассчитаем параметр λjk.
Предположим, что для страницы j наблюдаемая продолжительность визита 1/λj. Допустим, λjk подчиняется поправочной партнёрской функции (discounting function) Ljk (22):
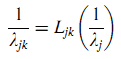
Поправочная функция может иметь различный вид для различных отношений между сайтами. К примеру, используем функцию Взаимной Поправки (Reciprocal Discounting function) (23) с коэффициентом c:
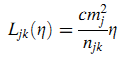
Затем можно рассчитать среднюю продолжительность визита в MobileRank как (24):

Из последней формулы видно, что а) чем больше число ссылающихся сайтов mj, тем меньше штраф средней продолжительности визита. б) при постоянном количестве ссылающихся сайтов, чем больше страниц сайта k ссылаются на цель, тем больше штраф средней продолжительности визита с сайта.
Гипотеза 3. Если параметры λj, j ∈ S одинаковы и поправочная функция имеет вид (25):
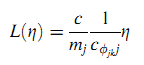
то MobileRank деградирует до PageRank.
Доказательство. Подставляя (25) в (22), а (22) в (17), получим (26):
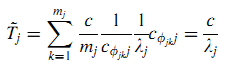
Так как в дальнейшем λ1 = λ2 = … = λn =Δ λ, а все Tj~ идентичны, то важность страницы зависит только от стационарного распределения вложенной цепи Маркова. Таким образом, получается эквивалент PageRank.
Из алгоритма конструкции ЗПМП видно, что сложность расчётов определяется доступностью страницы, оценкой полезности страницы и комбинацией авторитетности страницы. Расчёт доступности страницы схож со степенным методом PageRank и его сложность равна O(n2), где n — число страниц. Считая, что матрица переходов обычно весьма разрежена, настоящая сложность будет намного ниже значения O(n2). Для оценки полезности страницы при параллельном расчёте λjk необходимо только проверить (17). Расчётная сложность O(mn), где m = maxj=1, …, n mj, что намного меньше n. Комбинация авторитетности страницы рассчитывается через (2), сложность которой задаётся как O(n). Поэтому общая расчётная сложность предложенного фреймворка сравнима с алгоритмом PageRank и может успешно масштабироваться на крупных графах.
Алгоритм конструкции ЗПМП
Входные данные: веб-граф и метаданные.
Выходные данные: оценка авторитетности страницы π.
Алгоритм:
1. Сгенерировать матрицу вероятностей переходов P вложенной цепи Маркова из веб-графа и метаданных.
2. Рассчитать стационарное распределение π~ вложенной цепи Маркова, используя степенной метод. (доступность страницы).
3. Для каждой страницы j определить ссылающиеся на неё сайты и страницы, а затем рассчитать вероятность вклада cфkj.
4. Для каждой страницы j рассчитать параметр λjk из метаданных.
5. Рассчитать среднюю продолжительность визита Tj~ для каждой страницы j по (17). (полезность страницы).
6. Рассчитать авторитетность страницы в веб-графе по (9). (важность страницы).
Представив единый фреймворк мы обобщили PageRank, BrowseRank, BrowseRank Plus и обсудили прочие алгоритмы вида MobileRank. На рисунке 17 показана связь процессов Маркова и соответствующих алгоритмов расчёта важности страницы. Прямые линии от а к б означают, что а содержит б как свой частный случай. Пунктир от а к в означает, что алгоритм получен из а. Что касается процессов, видно, что Полумарковский Процесс и Зеркальный Полумарковский Процесс являются частными случаями Сетевого Скелетного Процесса Маркова, а непрерывный процесс Маркова является частным случаем и Полумарковского Процесса и Зеркального Полумарковского процесса. Дискретный Марковский Процесс является частным случаем непрерывного Марковского Процесса.
Рисунок 17. Связь процессов Маркова и алгоритмов расчёта авторитетности страницы (стрелками показано включение).
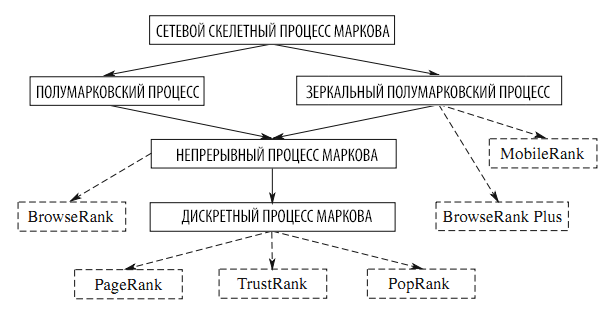
Касательно алгоритмов, видно, что PageRank, TrustRank и PopRank получены из дискретного процесса Маркова, BrowseRank — из непрерывного, а BrowseRank Plus и MobileRank из Зеркального Полумарковского процесса.
Подробности связей собраны в Таблицу 9. В ней приводится сводка условной вероятности yn и распределение yn по различным состоянияем Sn.
— В дискретном процесса Маркова, распределения yn по различным состояниям Sn являются детерминистическими, то есть средняя продолжительность визита считается константой.
— В трёх прочих случаях условной вероятности yn, если распределения yn по различным состояниям Sn различаются, то мы не обнаружили соответствующих алгоритмов расчёта авторитетности веб-страницы. Если распределения yn по различным состояниям Sn являются экспоненциальными, то они соответствуют непрерывному процессу Маркова, Полумарковскому Процессу и Зеркальному Полумарковскому Процессу, соответственно. Если распределения yn по различным состояниям Sn относятся к одному виду распределений, но не являются экспоненциальными, то они соответствуют процессам обновления (Papoulis и Pillai, 2001).
Таблица 9. Связь процессов Маркова и алгоритмов расчёта важности страницы.
| Условная вероятность yn | Распределение yn по различным состояниям Sn | Стохастический процесс | Алгоритмы | |
| Детерминистическое значение | Дискретный процесс Маркова | PageRank, TrustRank | ||
| Различные распределения | Экспоненциальное распределение | Непрерывный процесс Маркова | BrowseRank | |
| Один вид распределений | Другие | Процесс обновления | BrowseRank | |
| Различные распределения | Экспоненциальное распределение | Полумарковский Процесс | BrowseRank | |
| Один вид распределений | Другие | Процесс обновления | BrowseRank | |
| Различные распределения | Экспоненциальное распределение | Зеркальный полумарковский процесс | BrowseRank Plus, MobileRank | |
| Один вид распределений | Другие | Процесс обновления | BrowseRank Plus, MobileRank |
Полезная информация по продвижению сайтов:
Перейти ко всей информации