SEO-Константа
Яндекс.Директ + оптимизация
За последние несколько лет было предложено множество моделей для прогнозирования кликов пользователей поисковых систем. Кроме того, на основании пользовательской модели было создано несколько метрик оценки качества информационного поиска. В данной работе мы совмещаем эти два направления и предлагаем общий подход к конверсии любой кликовой модели в оценочную метрику. Затем мы встраиваем итоговую метрику на основании модели (наряду с традиционными метриками точности и DCG) в стандартный оценочный фреймворк и сравниваем их по нескольким направлениям.
Одно из направлений, в котором мы, в частности, заинтересованы — это согласование результатов онлайн и оффлайн экспериментов. Широко распространено мнение, что онлайн эксперименты A/B-тестирования и чередования (interleaving) лучше оценивают качество системы, чем оффлайн-измерения. Мы покажем, что оффлайн-метрики, основанные на кликовых моделях сильнее коррелируют с результатами онлайн-экспериментов, чем классические оффлайн-метрики, в особенности в ситуациях, где нет полных данных о релевантности.
На сегодняшний день существует два основных подхода к оценке качества системы ранжирования. Первый способ называется методом Крэнфилда [17] и выполняется оффлайн. В нём используется набор запросов и документов, оцениваемых специально обученными людьми (асессорами). Затем системы ранжирования оцениваются путём сравнения их результатов ранжирования – помимо всего прочего, считается, что система обязана помещать релевантные документы выше нерелевантных.
Второй подход, описанный Кохави и др. в [28] использует реальных онлайн пользователей, назначая часть из них в тестовые группы (так же называемые рейсами (flights)). Простейший вариант под названием A/B-тестирование, когда пользователи случайным образом распределяется в «контрольную» группу (которой показываются существующие результаты ранжирования) и «проверочную» группу (которой показываются экспериментальные результаты ранжирования). Затем системы ранжирования сравниваются посредством анализа кликов пользователей в «контрольной» и «проверочной» группах. По методу чередования (interleaving) Джоакимса [27] пользователям демонстрируется смешанный список результатов, составленный из обоих списков ранжирования. Затем система, которая получает больше кликов, признаётся лучшей из двух.
Одним из главных достоинств онлайн-оценки является то, что она основывается на пользователях и в результате, как часто считается, более точно показывается реальное качество системы. Эксперименты чередования широко используются такими коммерческими системами как Bing и Yahoo! [11, 31] и к тому же, изучаются в университетах [22, 32]. Однако онлайн-оценку трудно воспроизвести, в то время как классический подход Крэнфилда позволяет использовать тот же самый набор проверенных документов повторно для оценки любой системы ранжирования. Это делает неизбежным использование асессорских методов оффлайн-оценки на стадии ранней разработки алгоритмов ранжирования. Однако необходимо удостовериться, что итоговые асессорские оценки согласуются с результатами онлайн-экспериментов – онлайн-сравнение часто используется как последний проверочный шаг перед выпуском новой версии алгоритма ранжирования.
Чтобы сблизить эти два подхода мы предлагаем способ создания оффлайн метрики информационного поиска из модели кликов пользователей. Кликовые модели, вероятностные модели пользовательского поведения в сети, интенсивно изучались научным сообществом по информационному поиску в последние 5 лет. Главной целью прогнозирования кликов, как видно из предыдущих работ, является: (1) моделирование пользовательского поведения, когда использование реальных пользователей невозможно (см. [23]); (2) улучшение ранжирования с использованием релевантности, полученной из кликов (см. [10]). Наша гипотеза заключается в том, что кликовые модели можно использовать как оффлайн-метрику, а итоговая метрика на основе кликовой модели должна быть тесно связана с пользователем и, следовательно, должна лучше коррелировать с онлайн-измерениями, чем классические оффлайн-метрики. Более того, усиливается тенденция реализации оффлайн-метрики в пользовательской модели и это именно то, что пытается сделать моделирование кликов – предложить более хорошую модель пользователя. Встаёт вопрос: почему бы не использовать лучшие пользовательские модели на основе кликового поведения как фундамент оффлайн-метрики?
Наш вариант трансформации кликовой модели в метрику тщательно сравнивается с онлайн-измерениями. Наше сравнение включает в себя анализ корреляции с результатами эксперимента чередования, анализ корреляции с абсолютной онлайн-метрикой, анализ корреляции между классической оффлайн-метрикой и нашей новой метрикой на основе кликовой модели, а так же анализ степени дискриминации (discriminative power) различных метрик. Одним из направлений, которому мы уделяем особое внимание в нашем фреймворке сравнения, касается неоценённых документов. Как было показано Бакли и Вурхисом в [5] наличие частично оценённых страниц результатов в оценочном пуле может создать смещение в измерениях. Мы так же рассмотрим, как оффлайн-метрики справляются с этой проблемой. Так же покажем, что в ситуациях, когда невозможно использовать только полностью оценённые данные, мы по-прежнему можем использовать доступные данные для корректировок либо способом под названием конденсация [34], либо новым, предложенным нами методом предела.
Главные вопросы, рассмотренные нами в этой работе, таковы:
Нашим главным вкладом является метод конвертирования кликовых моделей в оффлайн-метрику на основе кликовых моделей. Кроме того, мы проводим тщательный анализ и сравнение конкретных метрик на основе кликовых моделей с онлайн-измерениями и классическими оффлайн-метриками.
Определение и сравнение качества систем информационного поиска всегда было важной задачей как в научной, так и в коммерческой областях. За последние несколько лет конкуренция между крупными коммерческими поисковыми системами достигла той точки, что даже небольшое улучшение может быть невероятно важным. Как итог, было предложено множество метрик измерения производительности системы: Discounted Cumulative Gain (DCG) за авторством Йарвелин и Кекалайнен [26], Expected Reciprocal Rank (ERR) от Чапелль и др. [10], Expected Browsing Utility (EBU) от Йилмаз и др. [39] и прочие. Им было найдено множество различных применений (см. [6, 10, 33]).
Некоторые метрики информационного поиска основаны на модели пользователя (см. ERR, EBU) или могут рассматриваться как таковые (см. [6]). Однако по-прежнему модели пользователей и метрики далеки друг от друга. К примеру, некоторые из широко используемых кликовых моделей, таких как Модель Сёрфинга Пользователя (User Browsing Model, далее — UBM) от Дупрета и Пивоварски [19] и Модель Зависимых Кликов (Dependent Click Model, далее — DCM) Гуо и др. [21] до сих пор не использовались для разработки оффлайн-метрик. Более того, с момента выпуска этих ранних кликовых моделей, было разработано множество других, не только как улучшения оригиналов [20, 30], но так же и реализующие конкретные цели моделирования, например, модель кликов для многоотраслевого поиска [12, 14], использование траекторий курсора наряду с кликами [24], а так же моделирование сессий [41]. Мы считаем, что все эти модели возможно сконвертировать в оценочные измерения.
Разработке классических тестовых наборов уделялось много внимания из-за небольших требований к ресурсам. Картеретт и Аллан [7], Сандерсон и Йохо [35] обсуждали методы построения тестовых выборок для оценки при низких затратах. Аззопарди и др. [3] и Берендсен и др. [4] пошли дальше и описали методики автоматической генерации тестовых коллекций и обучающего материала для систем ранжирования с обучением, соответственно. Прочие исследования концентрировались на одном из ограничений классических тестовых коллекций: полнота оценок [5, 34]. Бакли и Вурхис [5] представили новую метрику под названием bpref для использования в условиях отсутствия оценок релевантности. Сакай [34] предложил альтернативное решение, которое не требует новой метрики. Мы так же рассмотрим эту проблему при анализе метрик. Кроме оценочных метрик, возникают другие интересные вопросы при работе с крупными коллекциями запросов; они рассматриваются в работе «Million Query Track» [2] и изучаются далее в работе Картеретт и др. [8].
Следующая важная группа работ, тесно связанных с нашей, касается экспериментов над пользователями. Представленный Джоакимсом [27] метод чередования сегодня используется достаточно широко. С момента его создания было предложено несколько модификаций оригинального метода, среди которых стоит отметить Командное Чередование (Team-Draft Interleaving) [32] и Вероятностное Чередование (Probabilistic Interleaving) [22]. Способы чередования подробно рассматриваются в [11]. Радлински и Красвелл [31] анализировали и сравнивали чувствительность чередования и классической оффлайн-метрики информационного поиска друг с другом. Они обнаружили, что результаты экспериментов чередования, в основном, неплохо согласуются с оффлайн-метрикой, причём данные могут быть собраны при гораздо более низких затратах. Далее мы используем аналогичный метод анализа для оценки метрики на основе кликовой модели и её сравнения с классическими метриками информационного поиска. Али и Чен [1] показали, что по-запросная корреляция между оффлайновыми сравнениями и онлайновыми экспериментами чередования невысока в случае, когда применяется фильтрация запросов. Это открытие предполагает, что сбор результатов из нескольких запросов, как выполнялось в [31], менее зашумлен, чем расчёт корреляций на основе каждого запроса. Йу и др. [40] предлагают способы усиления сигнала эксперимента чередования; вдохновясь этой идеей, мы предлагаем регулировать оффлайн-метрику техниками под названием конденсация и предел для повышения согласованности с чередованием.
Со времени использования точности как метрики в качестве отправной точки, оценка информационного поиска существенно изменилась. Первым уроком было то, что требуется применять что-то наподобие скидки (discount) к документам, которые находятся ниже в ранжировании. Одной из первых метрик, которые оперируют этой идеей, является Discounted Cumulative Gain (DCG) [26]. Эта метрика до сих пор широко используется сообществом информационного поиска. Однако у неё есть определённые недостатки. Во-первых, функция скидки не определяется моделью пользователя. Во-вторых, это статическая метрика, т.е. значения скидки являются фиксированными. Как показано в [39], динамическая метрика, которая динамически назначает различные показатели скидки в соответствии с релевантностью документов, появляющихся выше в ранжировании, более точно отражает реальное пользовательское поведение.
В данной работе мы представляем понятие метрики на основе кликовой модели. Главной составляющей такой метрики является непосредственно кликовая модель – вероятностная модель для прогнозирования пользовательских кликов. Помимо событий клика (Ck) кликовая модель оперирует скрытыми переменными, соответствующими событиям вида «пользователь изучил сниппет k-го документа» (Ek). Эти скрытые переменные часто используются для более глубокого понимания пользовательского поведения. Например, Чапелль и Чан [9] используют кликовую модель (DBN) для прогнозирования релевантности и обучения функции ранжирования, а в [19] параметры кликовой модели анализировались для объяснения как предыдущие клики пользователя влияют на будущие клики. Все кликовые модели, которые рассматриваются в данной работе допускают, что пользователь кликает по документу только после изучения сниппета данного документа, т.е. P(Ck = 1|Ek = 0) = 0.
Вслед за Картеретт [6] мы проводим различие между метрикой полезности (utility-based) и метрикой действия (effort-based). Отсюда появляются два пути привязки кликовой модели к оффлайн-метрике на основе кликовой модели. Во-первых, метрика полезности использует кликовую модель только для прогнозирования вероятности клика P(Ck = 1) для k-го документа в ранжировании. Эта вероятность затем используется для расчёта оценочного значения ожидаемой полезности:
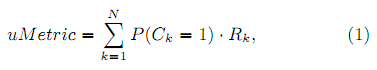
, где Rk – это релевантность k-го документа. Принято использовать 4-5 степеней релевантности от Нерелевантного до Высокорелевантного документа, которые затем конвертируются в численные характеристики. Например в [16] используется 4 уровня релевантности: от 0 (Нерелевантен) до 3 (Высокорелевантен) для каждого документа.
Во-вторых, метрика действия требует наличия в кликовой модели понятия «удовлетворённость пользователя» (Sk). Кликовая модель должна иметь скрытую переменную Sk, при этом должны соблюдаться условия P(Sk = 1|Ck = 0) = 0 (пользователь может быть удовлетворён документом только если он открыл его, т.е. кликнул) и P(Ej = 1|Sk = 1) = 0 для j > k (как только пользователь удовлетворён, он перестаёт исследовать документы). При наличии всего этого мы можем определить метрику как ожидаемое значение функции действия на точке остановки:
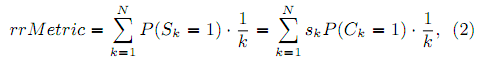
, где Sk = P(Sk = 1|Ck = 1) – вероятность удовлетворённости.
Кликовая модель обычно обучают по логу кликов. В результате мы получаем значения параметров модели, которые в дальнейшем можно использовать для расчёта вероятности кликов или событий удовлетворённости в уравнениях 1 и 2. Некоторые из этих параметров являются константами, некоторые зависят от позиции в ранжировании, а некоторые зависят от документа и/или запроса. Параметры последнего типа сложнее всего использовать в метрике, так как мы хотим, чтобы метрика работала даже для не виденных ранее документов. К счастью, такие параметры обычно могут быть аппроксимированы из релевантности документа. Фактически при обучении модели мы принимаем допущение, что эти параметры зависят только от релевантности документа, но не от самого документа. Мы продемонстрируем это для параметров привлекательности в DBN, DCM и UBM и параметров удовлетворённости в DBN.
Если модель отвечает требованиям, описанным выше, её можно трансформировать в метрику. Не существует пошагового алгоритма для такого конвертирования, есть только общие принципы. В последующих разделах мы проиллюстрируем эту идею, используя известные кликовые модели в качестве примера. Мы хотим особенно отметить, что наш фреймворк является достаточно обобщённым, чтобы применяться к остальным кликовым моделям, включая те, что используют дополнительные источники информации, например, недавно изученные кликовые модели на основе сессий [41] или кликовые модели для вертикального поиска [12, 14].
В Таблице 1 мы классифицировали ранее изученные метрики (ERR от Чапелль и др. [10], EBU от Йилмаз и др. [39]) и предложили несколько новых метрик на основе кликовых моделей: rrDBN, uDCM, rrDCM и uUBM. В крайнем левом столбце перечислены кликовые модели, центральный и крайний правый столбцы описывают оффлайн-метрики полезности и действия, соответственно. В качестве правил именования метрики мы используем имя фундаментальной модели, к которой добавляем префикс по типу метрики, которую мы определяем: u для метрики полезности (utility-based) и rr для обратного ранга (reciprocal rank) метрики действия. Обратный ранг (reciprocal rank) – это единица, делённая на значение ранга искомого элемента, т.е. просто обратное число ранга. Пример: предположим, имеется запрос для системы, которая выбирает множественную форму слова запроса из 3 ответов {Запрос: кошка; Ответы: кошкас, кошки, кошков}. Ранг правильного ответа – 2, следовательно, обратный ранг равен 0.5. Если в системе нет правильного ответа (его ранг равен 0), то и обратный ранг будет равен нулю.
Таблица 1. Метрики на основе кликовых моделей и их фундаментальные модели. Ранее предложенные модели/метрики обозначены ссылками на авторство.
| Фундаментальная кликовая модель | Производная метрика | |
| Полезность | Действие | |
| DBN [9] | uSDBN [10] | ERR [10] |
| DBN [9] | EBU [39] | rrDBN |
| DCM [21] | uDCM | rrDCM |
| UBM [19] | uUBM | – |
В данном разделе мы покажем как предложенные ранее метрики ERR и EBU могут быть рассмотрены в качестве метрик на основе кликовой модели. Несмотря на то, что эти метрики непохожи и что они, фактически, не являются производными кликовой модели, они обе могут рассматриваться как метрики, основанные на частном случае кликовой модели Динамической Сети Байеса (Dynamic Bayesian Network, DBN) за авторством Чапелль и др. [10]. В этой модели пользователь изучает сниппеты документа последовательно, один за другим и может быть привлечён документом u с вероятностью au. Если пользователь привлечён документом, он кликает по нему и затем с вероятностью su он может быть удовлетворён содержимым. Если пользователь не удовлетворён результатом, то он переходит к следующему документу с вероятностью γ, иначе он останавливается.
Метрика Expected Reciprocal Rank (ERR) использует упрощённую версию модели DBN [9] (далее по тексту – SDBN, Simplified Dynamic Bayesian Network), которая дополнена обязательным условием, что все вероятности привлекательности равны 1 (auk = P(Ck = 1|Ek = 1) ≡ 1) и только после этого все документы кликаются. Из этого следует, что suk ≡ ruk, т.е. вероятность удовлетворённости эквивалентна вероятности документа быть релевантным запросу. Делая это допущение, мы получаем вероятность клика по k-у документу:
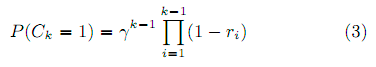
и вероятность удовлетворённости
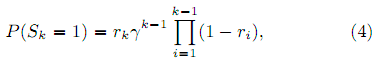
, где ri – вероятность релевантность i-го документа, а γ – вероятность продолжения. Вероятность документа быть релевантным обычно рассматривается как привязка R → r от уровней релевантности к значениям в пределе от 0 до 1. В исходной работе ERR [10] авторы используют привязку, похожую на DCG: r = (2R – 1)/2Rmax, где Rmax – максимально возможная степень релевантности, но так же можно использовать привязку из лога кликов.
Используя вероятности из уравнений 3 и 4, получим метрики ERR и uSDBN (по принципиальным уравнениям 2 и 1):
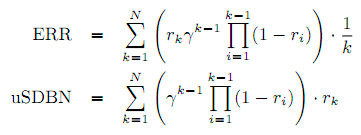
В оригинальной версии метрики ERR вероятность продолжения γ в модели DBN была установлена в 1. Мы же для uSDBN [10, Раздел 7.2] установим γ в 0.9 (1 минус вероятность отказа), как предложено в [9].
Метрика Expected Browsing Utility за авторством Йилмаз и др. [39] так же основана на вариации модели DBN. В отличие от оригинальной модели, модификация оперирует разными вероятностями продолжения в разных ситуациях (продолжение после клика, продолжение после нерелевантного документа, продолжение после релевантного документа). Эти параметры не только существенно повышают гибкость модели в настройке, но также и отражают сложность выбора пользователя. В исходной работе [39] они все были приведены в 1, мы поступим аналогичным образом, что приведёт нашу модель EBU к DBN [9] с вероятностью продолжения γ = 1. Следует отметить различие между метриками ERR и EBU: EBU не приравнивает вероятности привлекательности к 1. Вместо этого вероятности привлекательности и удовлетворённости оцениваются из лога кликов, используя допущение, что они определяются релевантностью документа:
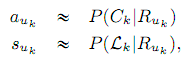
где Ck – случайная переменная, соответствующая клику по k-му документу, Lk – случайная переменная, соответствующая выходу со страницы результатов после клика по k-му документу, а Ruk – релевантность k-го документа uk.
В данном разделе мы предлагаем новые оффлайн-метрики, представив вариант метрики действия EBU и конвертируя две известных кликовых модели UBM и DCM в метрики на основе кликовой модели. Это покажет, что наш фреймворк метрики на основе кликовой модели является не только способом рассмотрения ранее созданных метрик, но так же и маяком для создания новых метрик для данного принципа.
Метрика rrDBN использует, в сущности, ту же пользовательскую модель, что и метрика EBU. Фактически, параметры EBU и rrDBN идентичны. Единственное отличие заключается в том, что rrDBN рассчитывается по Уравнению (2), а не (1).
Далее, метрики uDCM и rrDCM могут быть получены из DCM [21] способом, похожим на то как EBU и rrDBN получены из DBN. Отличие между DCM и DBN в том, что вероятность удовлетворённости P(Sk = 1) зависит не от самого документа, а от его ранга k в списке ранжирования. Таким образом, модель DCM может быть описана следующими уравнениями:
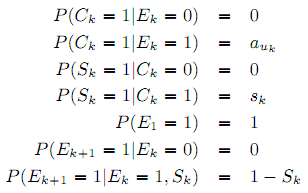
Как было показано Турпином и др. в [37], привлекательность сниппета документа может быть аппроксимирована как функция степени его релевантности. Привязка от уровней релевантности к вероятностям привлекательности может быть проведена из клика логов, используя кликовую модель (в данном случае DCM). Для этой цели мы налагаем обязательное условие, что документы с одинаковой релевантностью обладают одинаковой привлекательностью, т.е. привлекательность документа – это функция от уровня его релевантности: au = a(Ru).
Наконец, используя кликовую модель и Уравнения (1) и (2), можно определить метрики uDCM и rrDCM следующим образом:
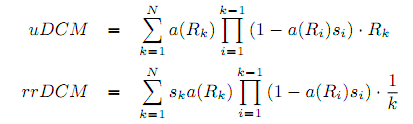
Чен и др. [12] сообщают, что User Browsing Model [19] работает лучше, чем DBN в вопросе сложности прогнозирования кликов. Мы так же оценили эту модель, используя лог кликов Яндекса. Мы использовали набор кликов, собранный в ноябре 2012. Мы исключили страницы без кликов и разбили отфильтрованные данные на обучающую и проверочную выборку. В итоге у нас было 1,191,963 обучающих и 1,292,993 проверочных страниц. Для сравнения этих моделей мы использовали прирост сложности (perplexity gain) [12, Раздел 5.2], что является стандартным способом сравнения значений сложности (см. [12, 20, 41]). На наших данных UBM превосходит DBN на 16%, что считается существенным.
Это мотивирует создавать оффлайн-метрику из UBM. В модели UBM вероятность клика зависит от смещения привлекательности и смещения исследования:
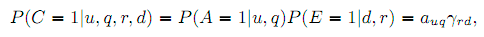
, где C – это клик, A – привлекательность, E – исследование документа; u – URL документа, q – запрос пользователя, r – ранг документа (позиция), а d = r–max{j < r|Cj = 1} – расстояние до предыдущего клика. Для простоты мы пишем ar вместо auq и γr(j) вместо γrd, где d = r–j.
Как и для метрик EBU/rrDBN и uDCM/rrDCM мы допускаем, что вероятность привлекательность a является функцией релевантности документа: auq = a(Ruq). Вероятности исследования γr(j) могут быть рассчитаны из логов кликов во время процесса обучения той же модели. Важно отметить отличие UBM от ранних моделей в том, что она полагается на предыдущие клики, а они недоступны в оффлайне. Для решения этой проблемы, мы разбиваем на множители вероятность P(Cr = 1) по позициям предыдущих кликов j:
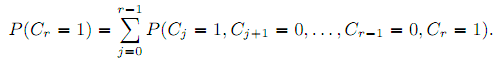
Применяя правило Байеса, получим:
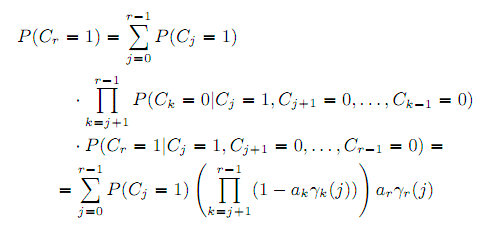
Наконец, вероятность клика определяется рекурсивной формулой:
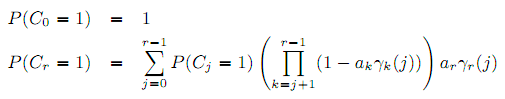
, где ar = a(Rr), а a(⋅) и γr(⋅) – известные функции, оцениваемые из кликов. Важно отметить, что в отличие от Дурпета и Пивоварски [19], мы использовали все запросы, а не только запросы с высоким показателем кликабельности. Поэтому наша итоговая функция γ отличается от анализируемой Дупретом и Пивоварски и может быть интересна сама по себе. К примеру, γr(j) намного меньше 1 для j > 0, что соответствует тому факту, что большинство пользователей кликают только по одному единственному документу.
При данной вероятности клика, можно определить метрику:
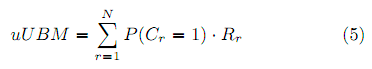
Кликовая модель UBM не располагает понятием удовлетворённости пользователя и, следовательно, мы не можем создать «rrUBM» метрику.
В данном разделе мы анализируем по ряду направлений старые и новые метрики на основе кликовых моделей. Мы сравниваем метрику на основе кликовых моделей с традиционными оффлайн-метриками. Под классическими метриками мы подразумеваем точность с двумя возможными бинаризациями четырёхуровневой оценки (Точность оценивает три высших оценки релевантности (3, 2, 1) как «релевантно», а Точность2 – только 2 оценки (3, 2) как «релевантно»), а так же DCG. Как было показано Чапелль и др. [10], метрика NDCG всегда хуже оценивает удовлетворённость пользователя, чем DCG. Мы решили не включать эту метрику и обойти потенциальные проблемы с нормализацией NDCG, зависящей от корпуса.
Начнём с определения корреляций различных оффлайн-метрик с результатами экспериментов чередования способом, предложенным Радлински и Красвеллом в [31]. Эти корреляции используются для последующего сравнения оффлайн-метрик друг с другом. Метрика, показывающая наилучшую корреляцию с результатами чередования считается наиболее точно отражающей реальное пользовательское поведение. Затем мы перейдём к более традиционным техникам стравнения, таким как корреляция метрика-к-метрике и степень дискриминации.
Как показали Радлински и др. в [32], абсолютные кликовые метрики зачастую неспособны определить отличия в системах информационного поиска. Более того, их всегда трудно интерпретировать и к тому же они могут быть ошибочны, так как нам неизвестно наверняка, как данные метрики относятся к удовлетворённости пользователя.
К счастью, существует ещё один подход: попарное или чередуемое сравнение, упомянутое ранее [27, 32]. По данному методу мы сравниваем две системы ранжирования, показывая пользователю смешанную страницу результатов, содержащую документы из обоих списков ранжирования. Победитель определяется по кликам пользователей. Мы оцениваем оффлайн метрику m по её согласованности с результатами чередования. В частности, мы используем метод Team-Draft Interleaving (TDI) от Радлински и др. [32]. В данном методе каждый документ на смешанной странице выдачи относится к одной из двух систем ранжирования («команд»). Мы считаем, что система побеждает в сравнении, если её документы на смешанной странице выдачи получают больше кликов. Система, победившая в большинстве сравнений считается лучшей.
Для данного эксперимента мы используем лог кликов поисковой системы Яндекс, собранный за период с октября по декабрь 2012. В этом периоде мы сосредоточились на 5 ревизиях ключевых функций ранжирования (A, B, C, D, E), сравнивая каждую ревизию с предыдущей, используя TDI в течение 5-10 дней. В каждом из наших 10 экспериментов у нас было как минимум 200,000 показов, как и в работе Радлински и Красвелла [31]. Некоторые ревизии функций ранжирования влияют более, чем на один сектор (страну), поэтому в общем у нас было 10 пар алгоритмов для сравнения: Δ1AB, Δ2AB, Δ1BC, Δ1CD, Δ2CD, Δ3CD, Δ4CD, Δ1DE, Δ2DE, Δ3DE. Для каждой пары алгоритмов мы записали значение сигнала чередования, т.е. отклонение от 50% случаев, когда предпочтительнее была новая система. Например, если эксперимент обозначен как ΔiXY и в нём система Y предпочтительнее системы X в 51% случаев, мы говорим, что сигнал чередования данного эксперимента составляет 1%.
Собрав сигналы чередования мы сможем сравнить их с сигналами, полученными оффлайн измерениями информационного поиска, т.е. среднее различие значений метрики. В отличие от классического подхода Крэнфилда, мы используем запросы и документы из лога запросов. При расчёте сигнала оффлайн-метрики для конкретного эксперимента ΛiXY мы извлекаем запросы, поданные пользователями, назначенными в экспериментальный «рейс». Для всех этих запросов мы так же извлекаем списки документов, которые были бы созданы системами X и Y, если бы не применялось чередование. Используя запросы на основе лога кликов при сравнении сигнала оффлайн-метрики с сигналом чередования мы устраняем эффект, вызванный выбором коллекции запросов, которую необходимо составлять для оценки по Крэнфилду. Так же это позволяет проводить эксперименты со старыми ревизиями алгоритмов ранжирования, которые больше не используются. И хотя этот подход обладает рядом преимуществ для нашей исследовательской задачи, он так же наделён недостатками в контексте ежедневного использования. Самым значительным из них является использование нами только части доступных оценок, так как не все запросы, по которым есть асессорские оценки, подавались целевой группой пользователей во время проведения эксперимента. Для каждого эксперимента и каждой метрики мы сохранили только те запросы, что имели как минимум один оценённый документ. В зависимости от эксперимента, в каждом из них было от 178 до 5,815 запросов (медиана 573). Как показано в [31], обычно хватает около 100 запросов для идентификации системы-победителя в оффлайн-сравнении.
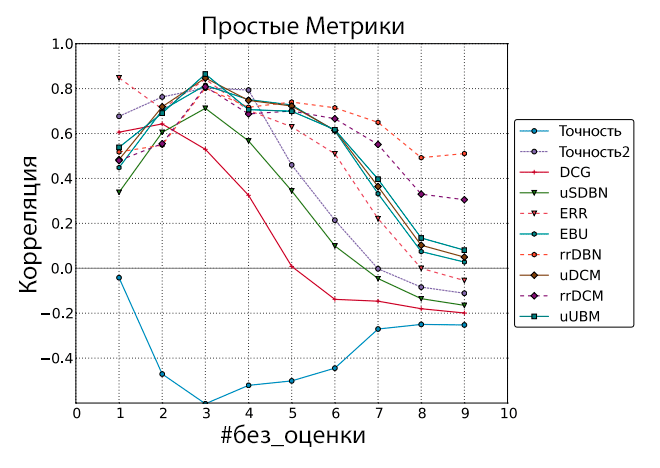
Рисунок 1. Корреляция Пирсона между оффлайн-метриками и сигналом чередования. Документы без оценки рассматривались как нерелевантные.
Объём информации, доступный поисковой системе уходит далеко за пределы человеческих возможностей по управлению данными. Более важно даже не это, а тот факт, что корпус Интернета постоянно меняется, из-за чего невозможно хранить итоговые оценки даже для небольшого количества запросов. Поэтому вполне естественно, что часть документов, выданная системой не имеет оценки релевантности. С целью анализа степени компромисса между добавлением шума от неоценённых документов и уменьшением шума посредством увеличения количества запросов, мы вводим новый параметр – #без_оценки (#unjudged). Мы исключаем запросы, для которых количество неоценённых документов в ТОП-10 больше такого количества в любой из двух систем, участвующих в эксперименте TDI. Далее мы регулируем это ограничение и наблюдаем его влияние на корреляцию между оффлайн-метриками и чередованием.
Для каждой оффлайн метрики m и каждого значения #без_оценки с 1 по 9 мы рассчитываем взвешенную корреляцию Пирсона (способом, похожим на [10]) между сигналом метрики и сигналом чередования. В качестве веса мы используем количество запросов, участвующих в расчёте сигнала метрики (это число варьируется для каждого эксперимента). Результаты показаны на Рисунке 1. Видно, что метрики действия rrDBN и rrDCM лучше справляются с документами без оценки и заметно отличаются от метрик полезности; мы рассмотрим это отличие в Разделе 4.3. Ещё одно интересное наблюдение касается метрик Точности и Точности2. Их поведение отличается и, более того, Точность обладает негативной корреляцией, чего нет у Точности2. Судя по всему, причиной этому служит тот факт, что документы без оценки обрабатываются так же, как и документы с нулевой релевантностью, хотя фактически у них намного больше шансов быть высоко релевантными запросу: 92% документов в ТОП-10 имеют степень релевантности выше 0, и только 23% имеют релевантность выше 1.
Рисунок 2. Корреляция Пирсона между оффлайн-метриками и сигналом чередования. Документы без оценки были пропущены (списки ранжирования конденсированы).
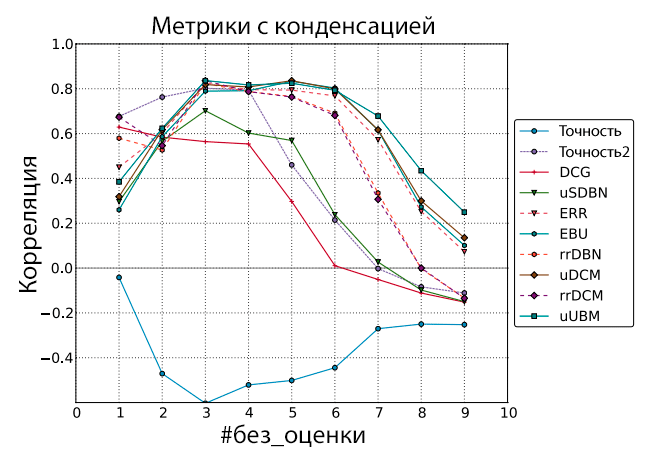
Как видно из Рисунка 1, при увеличении параметра #без_оценки (максимального количества документов без оценки) до 4 и выше, корреляция падает по всем исследуемым метрикам. Это означает, что добавление запросов с большим объёмом неоценённых документов зашумливает сигналы метрик. Проблема неоценённых документов ранее изучалась Сакай [34] и он предложил в качестве решения исключить документы без оценки из списка ранжирования и конденсировать остающиеся документы. Несмотря на свою эвристическую природу, эта идея увеличивает корреляцию для большинства метрик, как показано на Рисунке 2. Исключение из этого правила составляют rrDBN и rrDCM, которые, как и ожидается, страдают от некорректных значений функции действия. К примеру, если отсутствует оценка первого документа, то ко второму документу применяется скидка 1/1 вместо 1/2 (см. Уравнение 2).
Даже если применять конденсацию, корреляция по-прежнему падает при высоких значениях #без_оценки. Можно решить эту проблему выбрав оптимальное значение #без_оценки и постоянно используя его для получения высокой корреляции с результатами чередования. Однако мы предлагаем иной способ работы с зашумленными данными. Сравнивая систему A с системой B мы исключаем все запросы с разницей в метрических значениях меньше порога δm для каждой метрики m:
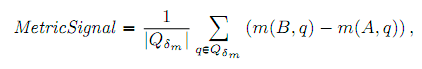
, где Qδm = {q ∈ Q | |m(B,q)–m(A,q)|≥ δm}. Это значит, что мы используем только небольшую долю запросов от всех имеющихся (до 20%), но это запросы, чётко распределённые между системами. Идея в том, что при выборе подходящего предела δm можно настроить систему ранжирования на максимальную корреляцию с результатами чередования. Чтобы протестировать идею, мы разбиваем наши данные (10 TDI экспериментов) на обучающую и проверочную выборку: обучающая выборка используется для выбора наилучшего порогового значения, а проверочная выборка нужна для расчёта значений корреляции.
Очевидно, что естественно разделять выборки по времени, однако это было бы непрактично при работе с нашими данными. Во-первых, невозможно получить обучающую и проверочную выборку адекватных объёмов (одна из них будет состоять только из 3 экспериментов, что приведёт к чрезмерной зашумленности значений корреляции). Во-вторых, возможно совсем немного вариантов разбиения по времени, поэтому мы не способны оценить статистическую важность результатов. Вместо этого мы использовали все возможные 5/5 разбиений для наших экспериментов, т.е. мы выбираем 5 из них в качестве обучающей выборки, а остальные назначаем проверочной. В целом у нас было C105 = 252 разбиения и соответствующих значений корреляции. Значения корреляции были усреднены, а ошибка рассчитывалась через метод bootstrap с уровнем уверенности в 95% используя 1000 образцов. Результаты показаны на Рисунках 3 и 4.
Рисунок 3. Корреляция Пирсона между оффлайн-метриками с лимитом и сигналом чередования. Документы без оценки рассматривались как нерелевантные.
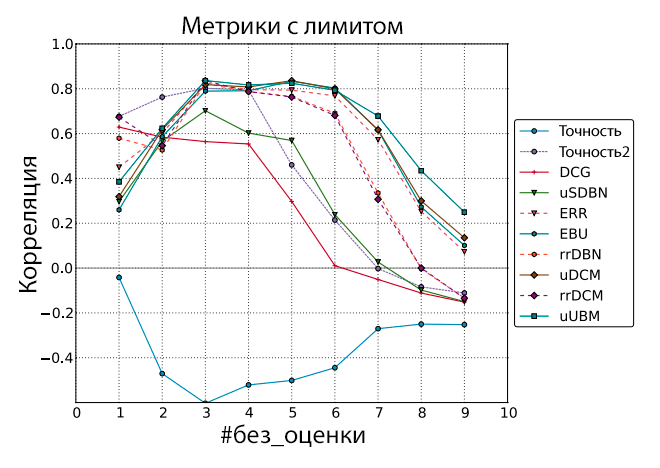
Рисунок 4. Корреляция Пирсона между оффлайн-метриками с лимитом и сигналом чередования. Документы без оценки были пропущены (списки ранжирования сконденсированы).
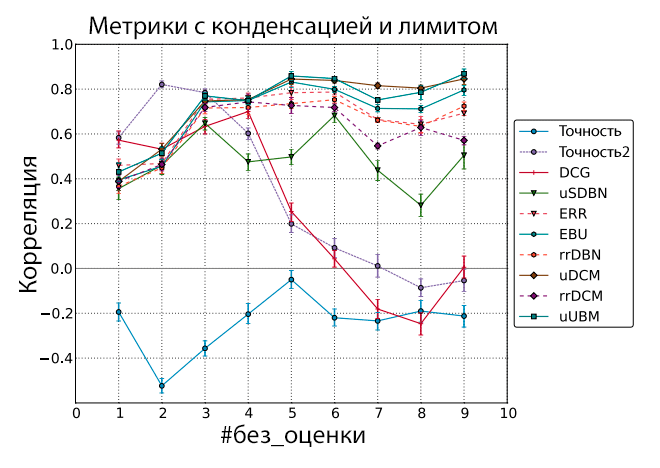
Из рисунков 3 и 4 видно, что интервалы уверенности довольно узки, а большинство метрик на основе кликовых моделей продолжают выдавать высокие значения корреляции при большом значении параметра #без_оценки. Если взглянуть на одну из наиболее производительных метрик uUBM, то видно, что значения с использованием порога немного хуже при параметре #без_оценки ниже 5, а при #без_оценки равном 5 и выше, варианты с использованием лимита начинают доминировать, достигая своего максимума при значении параметра #без_оценки = 9 (см. Рисунок 5).
Рисунок 5. Корреляция Пирсона между uUBM (в различных вариантах) и сигналом чередования.
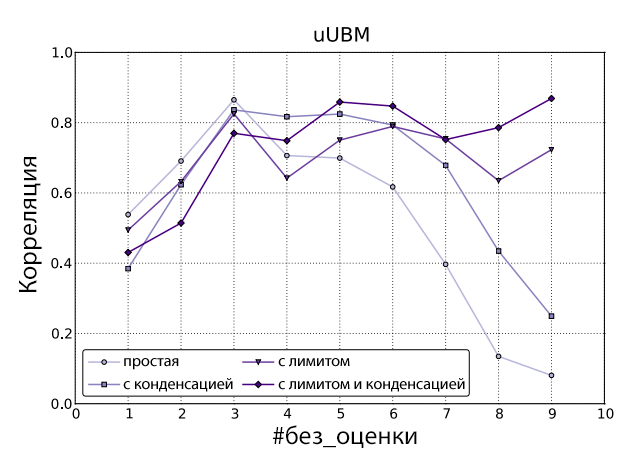
Чтобы протестировать важность различий между значениями корреляции, мы использовали процесс 5/5-разбиения, описанный выше. В отличие от того, что мы делали для вариантов с порогом, вариантов с порогом и конденсацией, для простого и конденсированного вариантов мы пользуемся только проверочной выборкой для определения корреляции и просто игнорируем обучающую выборку, в которой нам попросту нечего настраивать. Значения корреляции затем усредняются, а интервалы уверенности рассчитываются с использованием метода bootstrap по 1000 образцов со степенью уверенности в 95%. Три максимальных значения корреляции показывает вариант метрики uUBM с порогом и конденсацией (для разных значений #без_оценки), причём значение корреляции для метрики uUBM с порогом и конденсацией при параметре #без_оценки = 9 значительно выше любых других вариантов (простой, конденсированный, с порогом) метрик. Из Рисунков 1-4 можно сделать вывод, что метрики на основе кликовых моделей в целом показывают более высокие значения корреляции с результатами экспериментов чередования, чем классические оффлайн-метрики, в особенности при наличии множества документов без оценки (более 5), что подтверждает гипотезу, сформулированную во разделе «Введение»: метрики на основе кликовых моделей лучше коррелируют с онлайн-измерениями, чем традиционные метрики. Следующее интересное наблюдение заключается в том, что для простого и конденсированного вариантов существуют оптимальные значения параметра #без_оценки (3 и 5, соответственно, в данном случае). А для вариантов с порогом и с порогом и конденсацией важнее подобрать подходящую метрику и затем использовать любое значение #без_оценки, превышающее 5.
Как и в оригинальной работе Чапелль и др. [10] по ERR мы так же сравнили оффлайн-метрики с онлайн-метриками по значению корреляции. В наших экспериментах использовались следующие метрики:
Мы не включили метрику Удачности Поиска (Search Success, SS), учтённую Чапелль и др. в [10], так как она использует релевантность, а не только клики. Мы так же подтвердили открытия из [10], что QCTR (количество кликов на сессию) обладает отрицательной или близкой к нулю корреляций со всеми асессорскими метриками и она так же не включена в работу.
Конфигурация – это кортеж, состоящий из запроса и 10 URL, ранжируемых выше всего и показываемых пользователю. Для каждой конфигурации в нашем наборе данных были рассчитаны значения абсолютных онлайн и оффлайн-метрик. Вектора значений данных метрик затем были использованы для расчёта корреляции Пирсона (невзвешенный). Для нашего набора данных мы использовали клики, собранные в течение 3 месяцев в 2012. Так как мы использовали длительный период и, следовательно, обладали достаточным объёмом данных, мы сумели подобрать 12,155 конфигураций (соответствуя 411 уникальным запросам), в которых все 10 документов были оценены.
Результаты записаны в Таблице 2. Похожее сравнение проводилось ранее Чапель и др. [10] для ERR и классических оффлайн-метрик. Они получили значение, похожие на наши результаты. Из таблицы можно сделать вывод, что метрики на основе кликовых моделей показывают относительно высокие значения корреляции, а классические оффлайн-метрики DCG или Точности в общем имеют меньшую корреляцию, что согласуется с результатами предыдущего раздела. Используя проверку bootstrap (95% степень уверенности, 1000 образцов) мы подтвердили, что все метрики на основе кликовых моделей показывают значительно более высокую корреляцию со всеми онлайн-метриками по сравнению с любой традиционной оффлайн-метрикой.
Что касается онлайн-метрик, видно, что метрики с обратными рангами (MaxRR, MinRR, MeanRR) лучше коррелируют с метриками действия (ERR, rrDBN, rrDCM), так как функция действия, используемая данными метриками является обратным рангом 1/k (см. Уравнение 2). То же касается и PLC, использующего обратный ранг самого низкого клика, который можно рассматривать «точку удовлетворённости», используемую метрикой действия. Различия между ERR и uSDBN, rrDBN и EBU, rrDCM и uDCM являются статистически важными (при использовании тестирования bootstrap). Касательно метрики UCTR все метрики полезности показали значительно более высокую корреляцию по сравнению с метриками действия.
Мы так же сравнили новую метрику на основе кликовой модели со старыми метриками: ERR (метрика действия) и EBU (метрика полезности). Результаты сравнения отмечены верхними индексами в Таблице 2: первый соответствует ERR, второй – EBU. Первый (второй) ^ означает, что метрика статистически превосходит ERR (EBU), v – значительно уступает, а «-» означает отсутствие статистического отличия (95% уровень значимости по тесту bootstrap). Как можно заметить, в большинстве случаев наша новая метрика на основе кликовой модели работает лучше ERR и EBU, кроме меры UCTR, которая не считается за клики (скорее, за их отсутствие) и, следовательно, не имеет источников корреляции с метрикой на основе кликовой модели. По другим метрикам rrDBN и rrDCM лучше ERR в 3 случаях из 4 и лучше, чем EBU во всех 4 случаях, причём uUBM лучше EBU в 4 случаях из 4.
В целом, все абсолютные кликовые метрики плохо коррелируют с оффлайн-метриками – значения корреляции намного ниже корреляции с результатами чередования. Как было показано Радлински и др. в [32], абсолютные кликовые метрики хуже определяют удовлетворённость пользователя, чем чередование. Поэтому мы предлагаем использовать результаты из раздела 4.1 как основной способ сравнения оффлайн-метрики с пользовательским поведением.
Таблица 2. Корреляция Пирсона между оффлайн и абсолютными онлайн-метриками. Верхними индексами обозначены статистически важные отличия от ERR и EBU.
| Метрика | MaxRR | MinRR | MeanRR | UCTR | PLC |
| Точность | –0.117 | –0.163 | –0.155 | 0.042 | –0.027 |
| Точность2 | 0.026 | 0.093 | 0.075 | 0.092 | 0.094 |
| DCG | 0.178 | 0.243 | 0.237 | 0.163 | 0.245 |
| ERR | 0.378 | 0.471 | 0.469 | 0.199 | 0.399 |
| EBU | 0.374 | 0.467 | 0.464 | 0.198 | 0.397 |
| rrDBN | 0.384ΔΔ | 0.475ΔΔ | 0.473ΔΔ | 0.194∇∇ | 0.399—Δ |
| rrDCM | 0.387ΔΔ | 0.478ΔΔ | 0.476ΔΔ | 0.194∇∇ | 0.400—Δ |
| uSDBN | 0.322∇∇ | 0.412∇∇ | 0.407∇∇ | 0.206ΔΔ | 0.370∇∇ |
| uDCM | 0.374∇∇ | 0.466∇∇ | 0.463∇∇ | 0.198— | 0.396∇∇ |
| uUBM | 0.377—Δ | 0.469∇Δ | 0.467∇Δ | 0.198— | 0.398—Δ |
С целью сравнения оффлайн-метрик друг с другом в сфере ранжирования систем информационного поиска, мы использовали данные из [16]. Участникам соревнования TREC 2011 был предложен набор запросов и набор документов для каждого запроса, которые было необходимо отранжировать. Каждый документ оценивался по 4-уровневой шкале. Для каждой метрики мы можем построить список запусков системы, упорядоченный по усреднённому значению метрики по запросам. Затем мы рассчитываем значения корреляции расстояния Кендалла между данными отсортированными списками; они собраны в Таблице 3. Как было показано Вурхисом в [38], метрики со значениями корреляции около 0.9 могут считаться очень похожими, так как это значение, которое необходимо получить при использовании одной и той же метрики, но разных оценок. Этот уровень корреляции для различия эквивалентных метрик так же использовался в работах [5, 7, 35, 37].
В таблице 3 подобные пары метрик выделены жирным. Видно, что все метрики на основе кликовых моделей сильно коррелируют в пределах своей группы (группа метрик действия или полезности), при этом корреляции пар метрик, основанных на одной и той же модели (uSDBN и ERR, EBU и rrDBN, uDCM и rrDCM) ниже.
Таблица 3. Корреляция между оффлайн-метриками (по данным TREC 2011). Значения, превышающие 0.9 выделены жирным.
| Метрика | Точность2 | DCG | ERR | uSDBN | EBU | rrDBN | uDCM | rrDCM | uUBM |
| Точность | 0.649 | 0.841 | 0.597 | 0.730 | 0.568 | 0.397 | 0.562 | 0.442 | 0.537 |
| Точность2 | – | 0.785 | 0.663 | 0.780 | 0.675 | 0.526 | 0.693 | 0.551 | 0.681 |
| DCG | – | – | 0.740 | 0.857 | 0.711 | 0.530 | 0.704 | 0.592 | 0.685 |
| ERR | – | – | – | 0.807 | 0.919 | 0.754 | 0.902 | 0.826 | 0.888 |
| uSDBN | – | – | – | – | 0.792 | 0.585 | 0.794 | 0.638 | 0.754 |
| EBU | – | – | – | – | – | 0.788 | 0.970 | 0.822 | 0.930 |
| rrDBN | – | – | – | – | – | – | 0.786 | 0.917 | 0.807 |
| uDCM | – | – | – | – | – | – | – | 0.813 | 0.947 |
| rrDCM | – | – | – | – | – | – | – | – | 0.841 |
Ещё одной мерой, часто использующейся для сравнения метрик, является степень дискриминации (Сакай [33]). Это достаточно спорный метод, так как высокие значения степени дискриминации не являются характеристикой хорошей метрики. Тем не менее, слишком низкие значения степени дискриминации могут служить индикатором слабой способности метрики различать системы ранжирования. Как было показано в работах [15, 36], степень дискриминации в значительной мере определяется выбором метода статистической проверки. Зная это, мы сконцентрируемся на методе bootstrap, так как у него меньше допущений о фундаментальном распределении. Результаты по данным, используемым в предыдущем разделе собраны в Таблице 4. Как и ожидалось, сильно коррелирующие пары метрик (rrDBN и rrDCM, а так же EBU и uDCM) характеризуются похожей степенью дискриминации.
Так же интересно отметить, что метрики действия ERR, rrDBN и rrDCM характеризуются меньшей степенью дискриминации, чем метрики полезности uSDBN, EBU и uDCM, соответственно. Возможно, это обуславливается тем фактом, что «скидка позиции» для метрик действия стремится к нулю быстрее, чем для метрик полезности и, следовательно, они более чувствительны к изменениями в конце списка результатов.
Таблица 4. Степень дискриминации различных метрик по методу bootstrap (степень уверенности 95%).
| Метрика | Степень дискриминации |
| Точность | 50.1% |
| Точность2 | 30.8% |
| DCG | 48.6% |
| ERR | 39.3% |
| uSDBN | 51.1% |
| EBU | 35.1% |
| rrDBN | 21.1% |
| uDCM | 34.7% |
| rrDCM | 26.0% |
| uUBM | 33.3% |
В данной работе нами предложен фреймворк метрики на основе кликовой модели для создания оффлайн-оценки на базе любой модели кликов. Отвечая на исследовательские вопросы, поставленные во введении, можно сказать, что:
Естественным развитием нашего фреймворка метрики на основе кликовой модели является добавление большего количества сигналов от асессоров. К примеру, можно попросить асессоров оценивать не только документы, но так же и их сниппеты – это уже практикуется некоторыми коммерческими поисковыми системами. Если это реализовать, то можно ликвидировать допущение о том, что привлекательность сниппета является функцией релевантности документа. Так как привлекательность тесно связана с релевантностью документа [37], критически необходимо использовать реальные оценки привлекательности, если нужно оценивать алгоритм сниппета, а не только ранжирование. Возможно, стоит включить суждения о привлекательности сниппета в метрику и заново оценить метрику на основе кликовой модели с учётом предложенных улучшений.
Так же интересно провести исследование положительных (хороших) отказов. Ли и др. [29] докладывают, что некоторые сниппеты могут быть достаточно хороши, чтобы дать ответ на запрос пользователя напрямую из поисковой системы со страницы результатов. Как было показано в [13], можно попросить асессоров указывать, содержит ли сниппет ответ на запрос пользователя (полный или частичный). Задача показалась асессорам довольно простой. Обладая подобными оценками можно модифицировать любую оценочную метрику, добавив положительный фактор (прирост) документам, сниппеты которых содержат требуемую пользователю информацию, поэтому для продвижения сайтов совсем необязательно прохождение на возвращенную поисковой машиной страницу в том случае, если в сниппет решает его задачу. Чтобы превратить это в метрику, мы назначаем прирост документам, которые были кликнуты (Ck = 1), а так же прирост документам, которые были изучены, но не привлекли пользователя (Ei = 1, Ak = 0).
Так же интересно исследовать применение кликовых моделей для документов без оценки или с неизвестной оценкой. К примеру, можно было бы модифицировать кликовую модель, добавив вероятность пропуска документа по причине отсутствия его оценки. Этот вопрос заслуживает дальнейшего исследования, поэтому мы рассмотрим его в будущих работах.
В данном материале мы показываем, что оффлайн-метрики способны сильно коррелировать с результатами чередования. Однако нам может потребоваться метрика, коррелирующая с удовлетворённостью пользователя. Некоторые шаги в этом направлении уже сделаны (см. исследование Хаффмана и Хохстера [25]), когда проводилось исследование по анализу смыслового значения релевантности, назначенной асессорами, для реального пользователя. Было бы интересно развивать это направление для сравнения оффлайн-метрик.
Мы бы хотели поблагодарить Катю Хофманн, Марию-Энрике Питц и анонимных рецензентов за их вклад в данную работу.
Это исследование частично обеспечивалось 7-й Программой Фреймворков Европейского Сообщества (FP7/2007-2013) по грантам #258191 (PROMISE Network of Excellence) и #288024 (проект LiMoSINe), Голландской Организацией Научных исследований (NWO) в рамках проектов #640.004.802, #727.011.005, #612.001.116, HOR-11-10, Центром Создания, Разработок и Технологий (CCCT), проектом BILAND, финансированном по программе CLARIN-nl, Датской национальной программой COMMIT, Сетевой Исследовательской Программой ELIAS ESF, проектом Elite Network Shifts, финансированном Датской Королевской Академией Наук (KNAW) и Голландским Центром eScience в рамках проекта #027.012.105.
Материал «Click Model-Based Information Retrieval Metrics» перевел Роман Мурашов
Полезная информация по продвижению сайтов:
Перейти ко всей информации