SEO-Константа
Яндекс.Директ + оптимизация
Исследование методов машинного обучения в задачах ранжирования на основе конкурса «Интернет-математика 2009».Основные используемые методы. Сравнение результатов применения трех алгоритмов – Support Vector Machine (Машина опорных векторов), Random Forest (Случайный лес), Stochastic Gradient Boosting (Стохастический градиентный бустинг).
Одной из основных задач поисковых машин является ранжирование проиндексированных документов в соответствии с их релевантностью поисковому запросу пользователя. С развитием таких гигантов, как Яндекс, Google и Yahoo! постепенно усложнялись и алгоритмы поиска и ранжирования [от себя заметим, что во многом на данный процесс повлияло продвижение сайтов в их органической выдаче, так как ряд используемых для продвижения инструментов был нацелен на прямое ухудшение качества их поиска — прим. коллектива компании «SEO константа»]; на сегодняшний момент подавляющее большинство поисковиков работает по схеме, включающей в себя три основных этапа: непосредственно поиск документов, содержащих ключевой запрос, в том числе переформулированный, определение критериев оценки релевантности документа запросу и само ранжирование документов по степени релевантности запросу.
Самый распространенный метод выбора формулы ранжирования документов по степени релевантности – это машинное обучение, которое в основе своей предполагает использование определенных баз знаний. В качестве подобных баз знаний используются примеры оценки релевантности документа асессорами, которые точно так же руководствуются строго определенными критериями и признаками релевантности. Для корректных результатов в процессе машинного обучения использоваться должны достаточно обширные базы знаний вплоть до нескольких сотен тысяч примеров оценки релевантности асессорами на основе 100-1000 критериев ранжирования.
В этой статье вы ознакомитесь с описанием исходных данных, основными методами оценки и действующими метриками для оценки качества ранжирования. Кроме того, в этом материале приведены описания и сравнения использованных методов ранжирования, а также планы будущих исследований.
Компанией «Яндекс» весной 2009 года был проведен конкурс «Интернет-математика», непосредственно затрагивающий проблему ранжирования документов в соответствии со степенью их релевантности. Основной задачей участников было предложение формулы ранжирования на основе предоставленных организаторами общих алгоритмов и данных. Работа велась на основании значения признаков в парах типа «запрос-документ» и оценки степени их релевантности, установленной асессорами компании «Яндекс». Исходные данные включали в себя порядка 245 признаков из интервала [0;1], а также оценку релевантности документов асессорами от 0 до 4, где 0 – это нерелевантный документ, а 4 – высокая степень релевантности. Строгое определение и описание критериев оценки, т.е., признаков релевантности, участникам не предоставили, однако при этом в качестве критериев оценки использоваться могли любые признаки – длина запроса, частота его встречаемости в самом документе и т.п.
База данных для машинного обучения содержала 97290 строк (9124 запросов), а множество примеров для тестирования порядка 21103 строк (2026 запросов).
Основные методы оценки релевантности документа поисковому запросу
Практически все используемые сегодня методы оценки релевантности можно отнести к одной из трех основных категорий [2] – точечные методы, методы на списках и на парах. Основы каждой группы методов мы рассмотрим подробнее.
Точечные алгоритмы. В основе использования точечных методов лежит использование восстановление регрессии и обычной классификации документов по значению оценки отдельных признаков релевантности. Как примеры для машинного обучения используются пары типа «признак – значение релевантности» (xi;yi) для каждого документа. Наиболее существенным недостатком этого метода является независимая оценка каждого документа, в то время как ранжирование должно вестись с учетом признаков релевантности всех документов, соответствующих запросу.
Алгоритмы на парах.
Методы, основанные на использовании пар, в качестве примеров для машинного обучения рассматривают несколько иные типы объектов вроде Rij = ((xi,yi),(xj,yj)). Основной задачей является классификация пар на классы по типу «правильное ранжирование – неправильное ранжирование». Объекты типа Rij по сути описывают запросы по принципу «признаки – значение релевантности» (по типу (xi,yi),(xj,yj)). Этот метод ранжирования обладает тем же недостатком, что и точечный метод – независимая оценка документа без оценки прочих документов по запросу.
Алгоритмы на списках. Наиболее точным методом ранжирования документов в соответствии с релевантностью запроса является метод на списках, который анализирует и использует в качестве базы знаний для машинного обучения списки документов, соответствующих поисковому запросу.
Согласно условиям конкурса, в работе использовались только точечные методы ранжирования, что связано с их простотой, достаточно простой реализацией, а также высокой скоростью обработки.
| Метод и модель | Ссылки на публикации |
| Точечные алгоритмы | |
| McRank | [12] |
| Алгоритмы на парах | |
| Ranking SVM | [5] |
| RankNet | [1] |
| Алгоритмы на списках | |
| AdaRank | [9] |
| ListNet | [13] |
| ListMLE | [13] |
| RankGP | [8] |
Таблица 1 Алгоритмы и ссылки на публикации
Метрика эффективности формул ранжирования
Сегодня для оценки качества формул ранжирования используется огромное количество метрик, среди которых особо выделить можно Discounted Cumulative Gain (DCG), Normalized Discounted Cumulative Gain (NDCG), Mean Average Precision (MAP) [7]. Согласно условиям проводимого конкурса, в качестве метрики качества участниками использовалась DCG следующего вида:
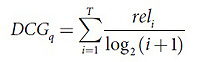
Здесь rel – это асессорская оценка документа, который стоит на i-ом месте в ранжированном посредством специальной формулы списке, T – это общее количество документов в списке, а q – это запрос.
Конечный результат усредняется с учетом всех запросов, поэтому чем выше конечное значение, тем, соответственно, и лучше работает формула ранжирования.
В следующей части статьи описаны три основных поисковых алгоритма, которые используются современными поисковыми машинами и которые в своей основе имеют точечные методы ранжирования.
Support Vector Machine. По сути, метод SVM на сегодняшний день является едва ли не самым популярным методом обучения, который активно используются и как метод простой классификации, и как метод восстановления регрессии. В основе этого метода лежит перевод исходных данных в пространство с большей размерностью [6]. В работе SVM использовался для восстановления регрессии, в частности, применялась реализация алгоритма из SVMlight.
| Тип Ядра | Discounted Cumulative Gain (DCG) |
| Линейное ядро | 4.165 |
| Полиноминальное ядро, d=2 | 4.229 |
| Полиноминальное ядро, d=3 | 4.233 |
| Полиноминальное ядро, d=4 | 4.232 |
| Полиноминальное ядро, d=5 | 4.219 |
| Полиноминальное ядро, d=6 | 4.219 |
Таблица 2 Результаты работы алгоритма SVM
Random Forest. Этот алгоритм машинного обучения предполагает группировку примеров для обучения в наборы случайных деревьев, причем качество и эффективность работы напрямую зависит от наличия ошибок каждого дерева, а также их некоррелированности [10], которая связана с применением техники бутстреп и использованием элементов случайности при построении.
Применение алгоритма на практике:
пусть p и N – количество примеров.
Для i=1,2….M
а) Создать выборку Θi с размерами N из N примеров с замещением (бутстреп)
б) На основе выборки Θi строится дерево Ti, в котором до минимального количества примеров в узле (менее nmin) повторяется рекурсивно следующий алгоритм действий для узлов:
Получение результата по формуле:
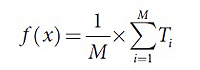
| M | nmin | Discounted Cumulative Gain (DCG) |
| 20 | 5 | 4.198 |
| 100 | 10 | 4.241 |
| 100 | 50 | 4.242 |
| 500 | 10 | 4.252 |
| 500 | 30 | 4.251 |
| 1000 | 10 | 4.248 |
| 1000 | 50 | 4.243 |
| 2000 | 30 | 4.248 |
Таблица 3 Результат работы алгоритма Random Forest
Stochastic Gradient Boosting. В основе SGB лежит все то же построение деревьев, однако здесь используются преимущественно простые деревья, количество листьев которых не превышает двадцати. Каждое дерево строится на остатках предыдущего [3].
Главной проблемой, с которой сталкиваются разработчики при подборе алгоритмов машинного обучения, является переобучение, для устранения которого в SGB используется модификация [4], позволяющая улучшить показатели качества и точности работы, а также скорость обработки алгоритма. Эта модификация выстраивает каждое дерево на основе случайных наборов примеров из всех приведенных примеров. Такой подход ( введение элемента случайности) позволяет в значительной степени повысить устойчивость алгоритма к переобучению, однако полностью проблема переобучения этим способом не решается. Кроме того, использование только части выборки для построения дерева повышает скорость работы.
Метод SGB с равным успехом используется и для простой классификации, и для восстановления регрессии. В ходе конкурса применялся алгоритм восстановления регрессии, предполагающий использование деревьев CART как базовых алгоритмов для обучения.
Описание используемого алгоритма:
L – функция штрафа, где для вычисления абсолютного отклонения используется распределение Лапласа, а для квадратичного – распределение Гаусса.
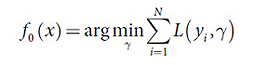
1. Инициализация:
2. Для m=1,2…,M:
а) Для i=1,2…,N найти:
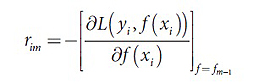
б) Построение дерева CART на основе набора {rim,xi}. Результатом построения являются области Rjm,j=1,2…Jm. Здесь Jm – это общее количество листьев построенного дерева.
в) Для полученной области j=1,2,…Jm необходимо посчитать значения в листьях:
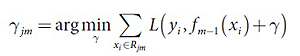
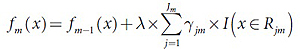
3. Результатом является ŷ(х)= fM(Х)
По итогам работы было установлено, что большей эффективностью обладает функция штрафа, использующая квадратичное, а не абсолютное отклонение. Сравнение результатов при разных значениях определенных параметров представлены ниже, в таблице №4.
| L | M | Jm | λ | Discounted Cumulative Gain (DCG) |
| Лапласа | 6K | 1 | 0.001 | 4.074 |
| Лапласа | 6K | 5 | 0.005 | 4.199 |
| Гаусса | 6K | 5 | 0.005 | 4.244 |
| Гаусса | 6K | 10 | 0.005 | 4.261 |
| Гаусса | 6K | 15 | 0.005 | 4.267 |
| Гаусса | 10K | 5 | 0.005 | 4.255 |
| Гаусса | 10K | 10 | 0.005 | 4.267 |
| Гаусса | 10K | 15 | 0.005 | 4.273 |
| Гаусса | 20K | 5 | 0.005 | 4.268 |
| Гаусса | 20K | 10 | 0.005 | 4.277 |
| Гаусса | 20K | 15 | 0.005 | 4.276 |
| Гаусса | 50K | 10 | 0.002 | 4.279 |
| Гаусса | 50K | 11 | 0.001 | 4.280 |
| Гаусса | 70K | 10 | 0.001 | 4.274 |
| Гаусса | 70K | 10 | 0.002 | 4.281 |
Таблица 4 Результаты работы алгоритма Stochastic Gradient Boosting
Согласно проведенным экспериментам, лучший результат (DCG=4.281) был достигнут при M=70000, где M – количество деревьев, и Jm, т.е., количестве листьев, равном 10. Параметр регуляризации здесь (λ) 0,002.
Рисунки 1 и 2 наглядно демонстрируют зависимость поведения метрики DCG и MSE (Mean Square Error) от количества построенных деревьев во время обучения и при проведении теста.
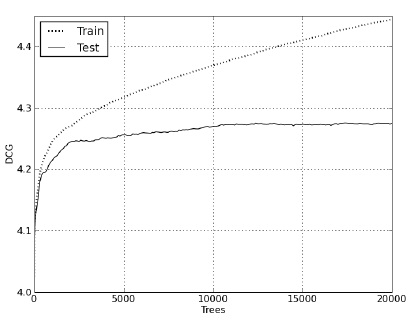
Рисунок 1 Поведение метрики DCG на тесте и на обучении
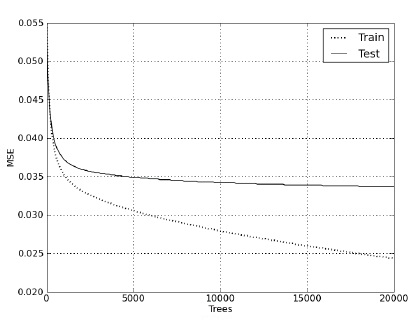
Рисунок 2 Поведение метрики MSE на тесте и на обучении
Результаты проведенных тестов привели к выводу, что оптимальным методом ранжирования из трех предложенных является Stochastic Gradient Boosting, так как результаты проверки эффективности алгоритма показали лучшие значения, чем у методов SVM и Random Forest.
Следующим этапом работ планируется сделать тестирование методов, использующих в своей основе пары и списки, а также провести ряд тестов, связанных с непосредственной оптимизацией самих метрик. Кроме того, планируется произвести тщательное исследование одного из наиболее перспективных подходов в методе SGB – метод прямой оптимизации метрики ранжирования (той же DCG), так как квадратичная метрика и метрика ранжирования слабо связаны. Конечно, прямым способом этого добиться невозможно, однако допускается использование аппроксимации метрики при помощи гладких функций.
Алексей Городилов (Яндекс, Москва)
Рерайт материала «Методы Машинного Обучения для Задачи Ранжирования» выполнила Инна Вдовицына
Полезная информация по продвижению сайтов:
Перейти ко всей информации