SEO-Константа
Яндекс.Директ + оптимизация
Система информационного поиска Google, которая использует алгоритм ранжирования интернет страниц, учитывающего не локальную, а глобальную гиперссылочную структуру посредством случайных блужданий, пользуется на сегодняшний день огромным успехом. В текущем материале предлагается простой универсальный алгоритм ранжирования как текстовых, так и графических данных, представленных в виде векторов в Евклидовом пространстве. Основная идея настоящего метода заключается в ранжировании информации с учетом внутренней связанной структуры объектов, составляющих эти данные. Обнадеживающие результаты проведенных нами экспериментов по искусственным, графическим и текстовым данным свидетельствуют о корректности предложенного подхода.
Поисковая система Google [2], осуществляет ранжирование страниц с помощью алгоритма PageRank, который учитывает при своих расчетах не локальную, а глобальную гиперссылочную структуру веба [1]. Интуитивно, это может быть представлено с помощью моделирования процесса случайного серфинга на веб-графе, при котором пользователь следует по некоторой последовательности гиперссылок случайным образом, а также периодически телепортируется на случайный веб-документ. При этом все интернет-странички ранжируются в соответствии со стационарным распределением вероятности случайного блуждания. Эмпирические результаты демонстрируют, что Google PageRank превосходит простое ранжирование, учитывающее сумму входящих гиперссылок на документ и, соответственно, использующее только локальную гиперссылочную структуру. От себя отметим, что успех данного алгоритма, привел к созданию различных модификаций, в том числе и небезызвестного тематического Индекса Цитирования Яндекса, который также косвенно учитывается при продвижении сайтов, и суть которого также сводится к нахождению левого столбца стохастической матрицы переходных вероятностей [прим. пер.]. Здесь нас интересует такая ситуация, при которой ранжируемые объекты (будь то графическая и/или текстовая информация) представлены в виде векторов в Евклидовом пространстве. Нашей целью является ранжирование данных в соответствии с внутренней глобальной структурой многообразия [6,7], извлекаемой из очень больших наборов данных. Мы полагаем, что для множества действительных типов данных, такой подход должен превосходить локальные методы, которые просто упорядочивают данные парными евклидовыми расстояниями или скалярным произведением векторов.

Рисунок 1. Ранжирование по двум фигурам, имеющих форму полумесяца. Размеры маркеров пропорциональны ранжированию, представленного в двух последних фигурах. Фигура (a) представляет собой модельный набор данных с единственным запросом; фигура (b) представляет собой ранжирование с учетом евклидова расстояния; (c) результат идеального ранжирования, которое мы стремимся получить.
Для того, чтобы объяснить нашу мотивацию, давайте взглянем на следующую модельную задачу. Пусть дано некоторое множество точек, формирующих две фигуры в форме полумесяца (Рисунок 1(a)). В верхнем полумесяце дан некоторый запрос, а наша задача состоит в том, чтобы отранжировать оставшиеся точки в соответствии с их релевантностью, касательно указанного пользовательского вопроса. Интуитивно, степени релевантности точек в верхнем полумесяце, касательно данного запроса, должны уменьшаться по мере нашего движения по этой фигуре. Это также справедливо и для точек, расположенных в нижнем полумесяце. Кроме этого, все точки, формирующие верхний полумесяц следует рассматривать как более релевантные для данного запроса, нежели чем те, что составляют нижнюю фигуру. Если мы отранжируем точки относительного данного запроса посредством евклидова расстояния, тогда крайние левые точки, формирующие нижний полумесяц, будут более релевантными нашему запросу, нежели чем те точки, что сформировали верхний полумесяц (Рисунок 1(b)). Очевидно, что такой результат не согласуется с нашей интуицией (Рисунок 1(c)).
Мы предлагаем простой универсальный алгоритм ранжирования, использующего внутреннюю связанную структуру данных. Этот метод является следствием наших недавних исследований в области частичного обучения с учителем [8]. В действительности, проблема ранжирования может быть рассмотрена как экстремальный случай частичного обучения с учителем, где нам доступны только положительные группы размеченных точек. Интуитивное описание нашего метода заключается в следующем. Сначала формируется взвешенная связанная структура данных; каждому запросу присваивается положительная ранжирующая оценка, а всем оставшимся точкам, которые также участвуют в процессе ранжирования по соответствующим запросам, назначается нулевое значение. Затем, все точки распространяют свои ранжирующие оценки через взвешенную связанную структуру своему ближайшему окружению. Процесс распространения повторяется вплоть до достижения устойчивого равновесного состояния всей системы, а все точки (за исключением запросов) ранжируются в соответствии с их окончательными ранжирующими оценками.
Оставшаяся часть материала организованна следующим образом. В Разделе 2 детально описывается наш алгоритм ранжирования. В Разделе 3 обсуждается связь с ранжирующим алгоритмом Google PageRank. В Разделе 4 вводится модификация классического алгоритма PageRank, которая способна ранжировать данные в зависимости от конкретных запросов. Наконец, в Разделе 5 представляются экспериментальные результаты, полученные по искусственным, графическим и текстовом данным; Раздел 6 подводит итоги настоящего исследования.
Для данного множества точек χ={x1,…, xq, xq+1,…, xn} ⊂ Rm, первые q точки являются поисковыми запросами, а оставшиеся — точками, которые нам необходимо отранжировать в соответствии с их релевантностью указанным запросам. Пускай d:χ x χ → R обозначает метрику по χ, такую, как Евклидово расстояние, которая назначает каждой паре точек xi и xj вес их лексической близости d(xi,xj). Пусть f:χ → R обозначает функцию ранжирования, которая присваивает каждой точке xi ранжирующее значение fi. Мы можем представить f как вектор f=[f1,…,fn]T. Мы также определяем вектор y=[y1,…,yn]T, где yi=1 в том случае, если xi является запросом; в противном случае yi=0. Если мы располагаем априорными знаниями, касающихся достоверности пользовательских запросов, тогда мы можем назначить им различные ранжирующие оценки, пропорциональные их достоверности. Алгоритм можно описать следующим образом:
Данный итеративный алгоритм может быть понят на интуитивном уровне. На пером шаге мы создаем связанную структуру. На втором шаге мы присваиваем ей веса, а на третьем — подвергаем их симметричной нормализации. Нормализация, используемая на третьем шаге, необходима нам для сходимости нашего метода. На четвертом шаге все точки распространяют свои ранжирующие оценки своему окружению, используя взвешенную структуру. Процесс распространения повторяется до тех пор, пока вся система не придет в состояние равновесия; на пятом шаге точки ранжируются в соответствии с окончательной ранжирующим значением. Параметр α определяет относительный вклад соседствующих точек в наши ранжирующие оценки, а также начальные ранжирующие значения. Стоит отметить, что благодаря установленному на втором шаге равенству диагональных элементов матрицы весов нулю, нам удается избежать самоусиления (self-reinforcement). Кроме того, так как S является симметричной матрицей, то и информация распространяется симметрично. Касательно сходимости нашего алгоритма, мы можем привести следующую теорему:
Теорема 1. Последовательность {f(t)} сходится к f*= β(I — αS)-1 y, где β=1-α. Строгое доказательство в работе [8]. Здесь мы только демонстрируем получение выражения в конечном виде. Положим f(t) сходится к f*. Подставляя f* вместо f(t+1) и f(t) в итерационном уравнении f(t+1) = αSf(t) + (1-α)y, имеем (1):
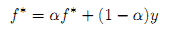
,которое может быть преобразовано следующим образом: (I-αS)f* = (1-α)y. Поскольку (I-αS) инвертируется, имеем: f* = (1-α)(I-αS)-1y. Очевидно отсутствие вклада в поставленную перед нами задачу ранжирования с стороны коэффициента масштабирования β. Следовательно, искомая нами конечная форма эквивалентна (2):
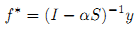
Мы можем использовать данный конечный вид для расчета ранжирующих значений точек напрямую. Но в решении крупномасштабных практических задач, мы, тем не менее, предпочитаем применять итерационный алгоритм. Наши эксперименты показывают, что нескольких итераций оказывается вполне достаточно для получения результатов ранжирования высокого качества.
Обозначим за G=(V,E) ориентированный граф, содержащий вершины. Пусть W обозначает матрицу смежности W, размером n×n, в которой Wij = 1 в том случае, если существует ссылка в E, исходящая из вершины xi к вершине xj; в противном случае Wij=0. Укажем, что матрица W возможно является несимметричной. Характеристика случайного блуждания по графу G определяется следующей матрицей переходных вероятностей (3):
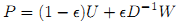
,где U является матрицей, все элементы которой равны 1/n. Это можно интерпретировать как вероятность ε перехода на смежную вершину, а 1-ε как вероятность телепортации в любую точку заданного графа равномерным случайным образом. Тогда, ранжирующие оценки по всем вершинам V, рассчитанные посредством PageRank, задаются стационарным распределением случайного блуждания. В нашем случае, мы будем рассматривать только неориентированный связанный граф. Очевидно, что в такой ситуации матрица W будет являться симметричной. Если, используя нашу методологию, мы также отранжируем все точки без соответствующих запросов так, как это делает Google, мы придем к следующей теореме:
Теорема 2. В задачах ранжирования данных, представленных в виде неориентированного связанного графа без запросов, f* и PageRank генерируют схожий результат ранжирования. Доказательство. Для начала покажем, что стационарное распределение π случайного блуждания, используемое в Google пропорционально степени вершины в том случае, если граф G является неориентированным и связанным. Пусть 1 обозначает вектор 1×n, все элементы которого равны 1. Имеем: 1DP = 1D[(1-ε)U + εD-1W] = (1-ε)1DU + ε1DD-1W = (1-ε)1D + ε1W = (1-ε)1D + ε1D = 1D. Пусть vol G обозначает величину графа G, определяемая как сумма степеней вершин. Тогда, стационарное распределение (4):
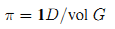
Обратите внимание на то, что π не зависит от ε. Следовательно, π также является стационарным распределением случайного блуждания, определяемого матрицей переходных вероятностей D-1W. Сейчас мы рассмотрим результат ранжирования, полученный с помощью нашего метода в ситуации отсутствия запросов. Итерационное уравнение, описанное на четвертом шаге нашего алгоритма, становится (5):
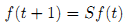
Классический вывод [4] линейной алгебры утверждает, что в том случае, если вектор f(0) неортогонален главному собственному вектору, тогда последовательность {f(t)} сходится к главному собственному вектору S. Пусть 1 обозначает вектор n×1, все элементы которого равны 1. Имеем: SD1/21 = D-1/2WD-1/2D1/21 = D-1/2W1 = D-1/2D1 = D1/21. Кроме того, отмечая, что максимальное собственное значение S равно 1 [8], мы знаем главный собственный вектор S, а именно D1/21. Следовательно (6):
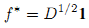
Если сравнить уравнения (4) и (5), становится очевидным, что f* и π генерируют схожие результаты ранжирования. Что и требовалось доказать.
Несмотря на то, что классический PageRank предназначен для ранжирования точек вне зависимости от какого-либо пользовательского запроса, мы можем легко модифицировать данную модель таким образом, что позволит нам решать проблемы запросо-зависимого ранжирования. Пусть P=D-1W. Ранжирующие оценки, присваиваемые PageRank, являются элементами решения сходимости итерационного уравнения (7):
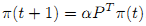
По аналогии с алгоритмом, представленным в Разделе 2, мы можем добавить пользовательский запрос в правую часть уравнения (7) в целях реализации запросо-зависимого ранжирования (8):
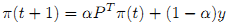
Это можно рассматривать в качестве персонализированной версии классического алгоритма Google PageRank. Мы можем показать, что последовательность {π(t)} сходится к π* = (1-α)(I-αPT)-1y как и прежде, что эквивалентно (9):
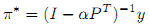
Теперь давайте проанализируем связь между (2) и (9) уравнениями. Заметим, что уравнение (9) может быть преобразовано в π*=[(D-αW)D-1]-1y=D(D-αW)-1y. Кроме того, f* может быть представлен как (10):
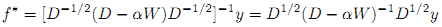
Таким образом, основное различие между π и f* заключается в том, что последнем из них, начальная ранжирующая оценка yi каждого запроса xi взвешивается относительно степени. Приведенные выше наблюдения мотивируют нас к предложению более обобщенного алгоритма персонализированного PageRank (11):
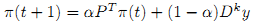
,где мы присваиваем запросам различную важность, в зависимости от их степени. Конечная форма (11) имеет следующий вид (12):
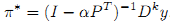
Если k=0, тогда уравнение (12) превращается в (9); в том случае, если параметр k=1, мы имеем π* = (I-αPT)-1Dy = D(D — αW)-1Dy, которое практически полностью соответствует уравнению (10). В задаче классификации мы также можем использовать уравнение (12) без какой-либо модификации, за исключением установки элементов y в 1 или -1, что будет соответствовать позитивной или негативной группе размеченных точек; и 0 для неразмеченных данных. Это показывает, что проблема ранжирования и классификации являются тесно связанными. Мы можем провести схожий с алгоритмом Клейнберга HITS [5] анализ отношений, который также является популярным алгоритмом ранжирования интернет-страниц. Основная идея данного метода также заключается в итеративном распространении ранжирующих оценок по существующему веб-графу. Мы опускаем дальнейшее обсуждения этой методологии по причине отсутствия свободного пространства в нашей работе.
Мы решили проверить пригодность нашего метода на одной искусственной и двух практических моделях, которые включают в себя ранжирование изображений и текстовой информации. В наших последующих экспериментах мы будем использовать выражение в конечном виде, где параметр α устанавливается на 0.99. Поскольку в данных задачах известна настоящая маркировка, то есть категории изображений и документов (в отличие от проблемы ранжирования результатов на практике) мы можем рассчитать ошибку ранжирования посредством использования ROC-оценки (Receiver Operating Characteristic) [3] для оценки производительности методологий. Возвращенная оценка будет заключена в диапазон от 0 до 1; значение равное 1 указывает на идеальный алгоритм ранжирования.
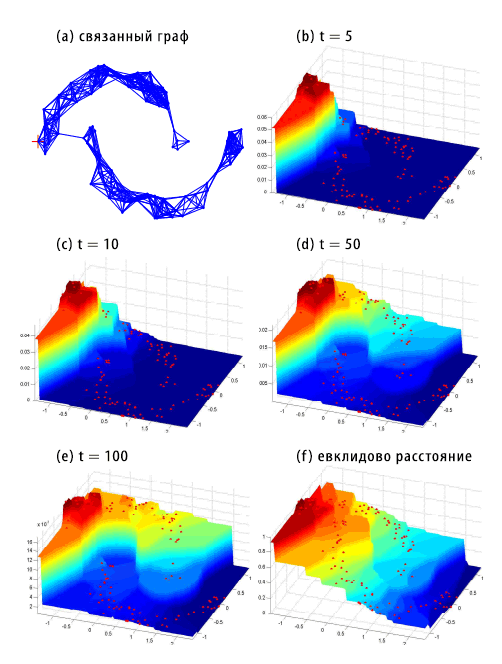
Рисунок 2. Ранжирование по фигуре, состоящей из двух полумесяцев. (a) связанный граф; (b)-(e) ранжирование с различными количеством шагов: t=5; 10; 50; 100; (f) ранжирование по евклидовому расстоянию.
Сейчас мы рассмотрим первую искусственную задачу, которая была упомянута во вступительной части нашего с вами материала. Связанный граф, описанный на первом шаге нашего алгоритма, представлен на Рисунке 2(a). Ранжирующие оценки с различным количеством шагов (t=5; 10; 50; 100) отражены на Рисунке 2 (b)-(e). Обратите внимание на то, что оценка релевантности, касательно заданного пользовательского запроса, будет уменьшаться по мере нашего продвижения по каждой фигуре в форме полумесяца; точки запросов, формирующие верхний полумесяц следует рассматривать как более релевантные для данного запроса, нежели чем те, что составляют нижнюю фигуру. Ранжирование по евклидовому расстоянию, которое не в состоянии охватить структуру, состоящую из двух полумесяцев, представлено на Рисунке 2 (f). Стоит отметить, что простое ранжирование данных по наикратчайшему пути [7], выполняется на этом графе недостаточно хорошо. В частности, мы хотим обратить внимание наших читателей на длинное ребро Рисунка 2(a), которое соединяет два полумесяца. Очевидно, что наикратчайший путь оказывается крайне чувствительным даже к несущественным изменениям графовой модели. Надежное решение состоит в сборе всех путей между двумя точками с последующим их взвешиванием с помощью убывающего фактора. Именно так мы и поступили. Обратите внимание на то, что конечное форма может быть расширена как f*= ΣiαiSiy.
Здесь мы ставим задачу ранжирования выборки рукописных цифр почтовой службы USPS размером 16х16. В этом эксперименте мы рассматриваем только подмножество цифр от 1 до 6. Для каждого класса мы имеем 1269, 929, 824, 852, 716 и 834 образцов; общее число образцов составляет 5424. Случайным образом мы выбираем образцы из одного класса цифр для включения их выборку запросов с более чем 30 испытаниями, а затем ранжируем оставшиеся цифры относительно указанных наборов. Для создания матрицы весов W мы используем ядро Радиальной базисной функции (RBF) с шириной α=1.25, однако диагональные элементы матрицы устанавливаются в ноль. Методология ранжирования по евклидовому расстоянию используется нами в качестве базиса: дается набор запросов {xs} (s∈S), точки x ранжируются по принципу: наибольший рейтинг присуждается точке x с наименьшей оценкой mins∈S||x-xs||.
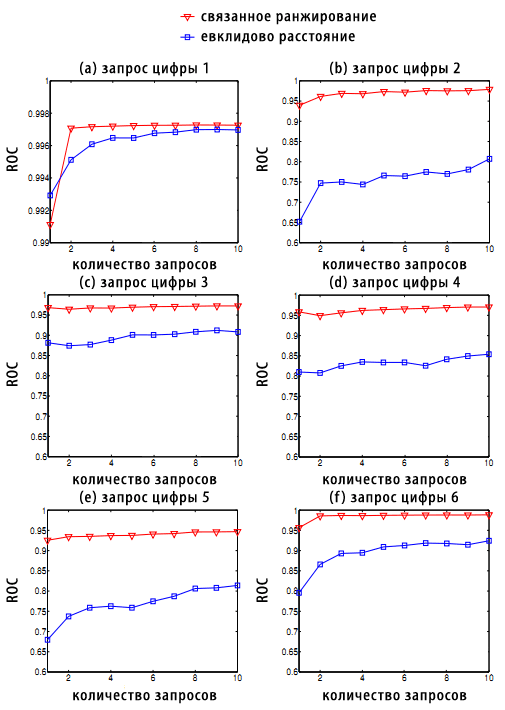
Рисунок 3. ROC-оценка по данным USPS по различным классам цифровых запросов. Обратите внимание, что текущие экспериментальные результаты также являются косвенным доказательством внутренней структуры многообразия данных USPS.
Результат, полученный в ходе ROC-оценки, приведен на Рисунке 3; каждый участок соответствует различным классам цифровых запросов от 1 до 6 соответственно. Наш алгоритм сравним с базисом в том случае, когда в качестве запроса выступает цифра 1. Однако для других значений используемый нами метод значительно превосходит базисную оценку. Этот экспериментальный результат также является косвенным доказательством внутренней структуры многообразия набора цифровых данных USPS [6,7].
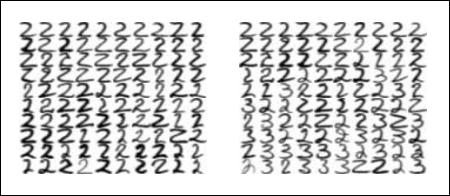
Рисунок 4. Ранжирование цифровых данных USPS. В качестве запроса выступает верхняя левая цифра на каждой панели. Левая панель демонстрирует топ 99 изображений, отранжированных с помощью алгоритма связанных структур; правая панель демонстрирует топ 99 изображений, отранжированных по евклидовому расстоянию. Отметим, что на правой панели намного больше двоек с завитушками.
На Рисунке 4 представлен топ 99 изображений, полученный с помощью нашего алгоритма и евклидова расстояния со случайной цифрой 2, использованной в качестве запроса. В качестве запроса выступает верхняя левая цифра на каждой панели. Обратите внимание на то, что в правой панели наличествуют несколько троек. Кроме того, на ней же присутствуют множество двоек с завитушками, которые не совсем хорошо соответствуют запросу. Видно, что 2-ки левой панели в большей мере соответствуют нашему запросу, нежели чем двойки правой. Данное неявное превосходство приобретает большое значение в практических задачах ранжирования, в которых пользователей интересуют в основном только несколько первых, наиболее высокоранжируемых результатов поиска. Однако метрика ROC оказывается слишком простой для того, чтобы отразить это не совсем явное превосходство.
В этом эксперименте мы исследуем задачу ранжирования текстовой информации, используя набор данных 20-ти новостных групп. Мы выбрали записи, которые содержали в себе такие темы, как автомобили, мотоциклы, бейсбол и хоккей из версии 20-news-18828. Статьи был обработаны пакетом программ Rainbow со следующими параметрами: (1) предварительный прогон всех слов через стример Porter до начала их подсчета; (2) исключение любого токена, содержащегося в стоп-листе системы SMART; (3) пропуск всех заголовков; (4) игнорирование слов, который встречаются в 5 или большем числе документов. Какой-либо дополнительной обработки на этапе предпроцессинга выполнено не было. Удалив пустые документы, мы получили 3970 документных векторов в 8014-мерном пространстве. В завершении всего, документы были нормализованы в представлении TFIDF. В качестве базиса мы используем метод ранжирования по нормализованному скалярному произведению векторов. Мы также создаем матрицу весов W с помощью скалярного произведения, то есть представляем в его виде линейное ядро. Оценка ROC для 100 рандомно выбранных запросов для каждого класса представлены на Рисунке 5.
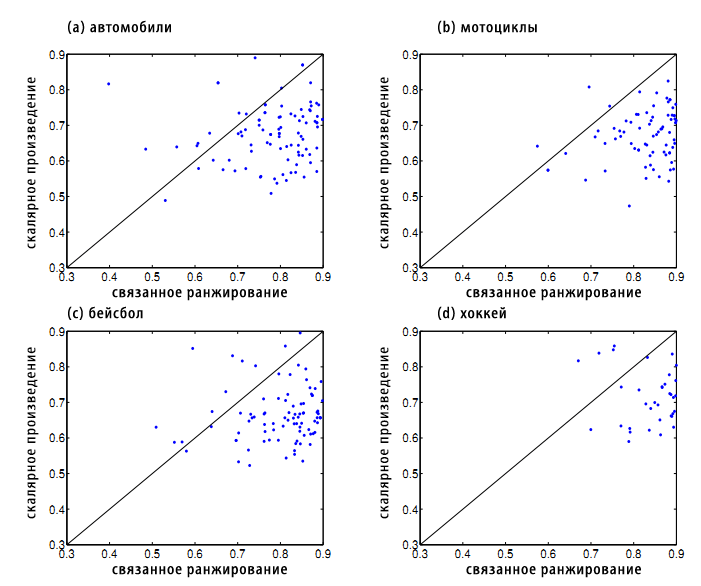
Рисунок 5. Оценка ROC разбросала фрагменты 100 случайных запросов, соотносящихся с такими категориями как автомобили, мотоциклы, бейсбол и хоккей, которые содержались в наборе данных 20 новостных групп.
В последующих исследованиях мы намереваемся изучить модель селекции. Потенциально, если мы располагаем незначительным размеченным набором или выборкой запросов, превышающей размер 1, в таком случае может быть использована стандартная технология кросс-валидации. Кроме того, это даст нам возможность исследовать теорию устойчивости алгоритмов для выбора соответствующих гиперпараметров. Также существует ряд возможных расширений для данного подхода. Например, мы можем реализовать фреймворк итеративной обратной связи: в том случае, если пользователь определяет положительную обратную связь, это может быть использовано для расширения выборки пользовательских запросов и улучшения выходных значений ранжирования. Наконец, самое главное заключается в том, что мы заинтересованы в применении текущего алгоритма в задачах решения крупномасштабных практических проблем систем информационного поиска.
Перевод материала «Ranking on Data Manifolds» выполнил: Константин Скоморохов
Полезная информация по продвижению сайтов:
Перейти ко всей информации