SEO-Константа
Яндекс.Директ + оптимизация
В отличие от стандартных задач классификации и метрической регрессии машинного обучения мы исследуем проблему прогнозирования переменных порядковой шкалы, называемой порядковой регрессией. Эта проблема часто возникает в области социальных наук и в сфере поиска информации, где предпочтения человека играют важную роль. В то время как подходы, предложенные в статистике, полагаются на вероятностную модель скрытой переменной, мы представляем распределение независимого формулирования рисков порядковой регрессии, что позволяет нам получить равномерную границу сходимости. Применение данной границы представлено алгоритмом большого отступа (large margin), который основан на отображении объектов в скалярной величине, таким образом, разбивая их по парам. Мы приведем экспериментальные результаты для задачи поиска информации, которые покажут, что наш алгоритм превосходит более примитивные подходы к порядковой регрессии, такие как классификация опорных векторов (Support Vector Classification) и регрессия опорных векторов (Support Vector Regression) в случае более двух рангов.
Приминая во внимание iid выборку (X, Y), и множество F отображений f: X → Y, процесс обучения стремится к поиску f*, что, используя предопределенные потери c: X x Y x Y→R, сводит функциональный риск к минимуму. Используя принцип минимизации эмпирического риска, выбирается функция femp, которая минимизирует среднее значение потерь Remp(f), заданных образцом (X, Y). Вводя количество, которое характеризует способность F, можно получить границы отклонения |R(femp) — inff∈FR(f)|. Рассмотрим два основных сценария: (i) Если Y является конечным неупорядоченным множеством (номинальная шкала), то оно относится к задаче классификации обучения. Поскольку Y является неупорядоченным, потеря 0-1, т. е. cclass(x,y,f(x)) = 1f(x)≠y, полностью удовлетворяет захвату потери в каждой точке (х, у). (ii) Если Y является метрическим пространством, например, множеством действительных чисел, то оно относится к задаче восстановления регрессии. В этом случае функция потерь может принять во внимание полную метрическую структуру. Различные метрические функции потерь, которые являются оптимальными в данной вероятностной модели P(y|x) были предложены в литературе (см. Хубер, 1981). Как правило, оптимальность выражается средним квадратом ошибки femp.
Рассмотрим проблему, которая обладает общими свойствами обоих случаев (i) и (ii). В (i) Y представляет собой конечное множество, а в (ii) элементы Y упорядочены. В отличие от задачи восстановления регрессии, мы имеем дело с тем, что Y не является метрическим пространством. Переменная вышеуказанного типа относится к порядковой шкале и может рассматриваться как результат грубо измеренной непрерывной переменной [Anderson и Philips, 1981]. Порядковая шкала приводит к проблемам в определении соответствующей функции потерь для нашей задачи (см. также McCullagh, 1980 и Anderson 1984). С одной стороны, не существует метрики в пространстве Y, т.е. расстояние (у — у’) из двух элементов не определено. С другой стороны, простая потеря 0 — 1 не отражает упорядочение в Y. Поскольку не может быть установлено никакой функции потерь c(x,y,f(x)), которая действует на истинные ранги y и прогнозированные ранги f(x), мы предлагаем использовать порядковый характер элементов Y, рассматривая порядок в пространстве X, вызванный каждым отображением f: X → Y. Таким образом, наша функция потерь c pref(x1, x2, y1, y2, f(x1), f(x2)) действует на пары истинных рангов (y1, y2) и прогнозированных рангов (f(x1), f(x2)). Такой подход позволяет сформулировать независимую теорию распределения порядковой регрессии и дать единые границы для функционального риска. Грубо говоря, предлагаемый функциональный риск измеряет вероятность неправильной классификации случайно взятой пары (x1, x2) наблюдений с двумя классами x1>xx2 и x2>xx1. Проблемы порядковой регрессии возникают во многих областях, например, в информационном поиске [Wong и соавт., 1988, Herbrich и соавт., 1998], в эконометрических моделях [Tangian и Gruber, 1995, Herbrich и соавт., 1999], и в классической статистике [McCullagh, 1980, Fahrmeir и Tutz, 1994, Anderson, 1984, de Moraes и Dunsmore, 1995, Keener и Waldman, 1985].
В качестве применения вышеупомянутой теории, мы предлагаем моделировать ранги интервалами на числовой оси. Тогда задача будет состоять в том, чтобы найти скрытую функцию выгоды, которая отображает объекты в скалярных значениях. В связи с упорядочением рангов, функция разграничивается транзитивностью и асимметрией, потому что они являются определяющими свойствами отношения предпочтений. Итоговая задача обучения также известна как обучение отношению предпочтений (см. Herbrich и др. 1998). Можно подумать, что обучение отношению предпочтений сводится к стандартной задаче классификации, если учитываются пары объектов. Это, однако, не соответствует действительности, потому что свойства транзитивности и асимметрии могут быть нарушены традиционными байесовскими подходами в связи с проблемой стохастической транзитивности [Suppes и др., 1989]. Учитывая пары объектов, задача обучения сводится к нахождению функции выгоды, которая лучше всего отражает предпочтения, вызванные неизвестным распределением p(x,y). Наш процесс обучения на парах объектов является идеей высокой исправляющей способности, известной из данных, зависимых от структурной минимизации риска [Shawe-Taylorи др., 1998]. Итоговый алгоритм похож на метод опорных векторов. Так как во время его обучения и применения должны быть вычислены только скалярные произведения представлений объекта xi и xj, можно применить метод потенциальных функций (см. Aizerman и соавт. 1964).
В этом разделе мы вкратце вспомним широко известную кумулятивную или пороговую модель порядковой регрессии [McCullagh и Nelder, 1983].
Мы предполагаем, что есть пространство исходов Y = {r1,… ,rq} с упорядоченными рангами rq>yrq-1>y…>yr1. Символ >y обозначает упорядочение между различными рангами, и его можно интерпретировать как «предпочтение к». Так как Y содержит только конечное число рангов, P(y = ri|x) является полиномиальным распределением.
Предположим, что стохастическую упорядоченность соответствующего пространства X, т. е. для всех различных x1 и x2, можно выразить как:
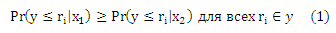
или
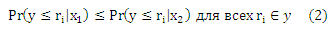
Стохастическая упорядоченность удовлетворяется следующей моделью:
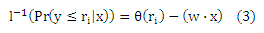
где l-1: [0,1] → (—∞,+∞) является монотонной функцией, которая более известна как инверсионная связывающая функция, и θ: Y → R возрастает пропорционально рангам. Стохастическая упорядоченность следует из того, что
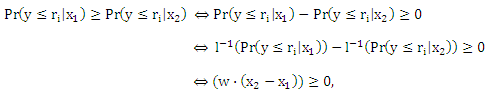
и более не зависит от ri (то же самое относится и к Pr(y ≤ ri|x1) ≤ Pr(y ≤ ri|x2)). Такая модель называется кумулятивной или пороговой моделью и ее можно обосновать следующим доказательством: Предположим, отклик грубо измерен скрытой непрерывной переменной U(х). Таким образом, мы наблюдаем ранг ri в обучающем наборе данных в том случае, когда
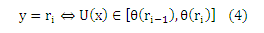
где функция U (скрытая полезность) и θ=(θ(r0),… ,θ(rq))T должны быть определены из данных. По определению θ(r0)= —∞ и θ(rq) = +∞. Мы видим, что ось разделена на q последовательных интервалов, где каждый интервал соответствует рангу ri. Создадим линейную модель скрытой переменной U(х)
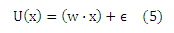
где ε является случайным компонентом нулевого математического ожидания, Eε(ε) = 0, и распределено по Pε. Из уравнения (4) следует, что
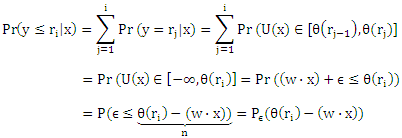
Если мы теперь сделаем предположение о характере распределения Pε для ε, то получим кумулятивную модель, выбрав в качестве инверсионной связывающей функции l-1 инверсионную функцию распределения Pε-1 (квантильную функцию). Заметим, что каждая квантильная функция Pε-1: [0,1] → (—∞,+∞) является монотонной функцией. Различные предположения о характере распределения для ε дают логит, пробит или дополнительную модель повторного логарифма (табл. 1).
Таблица 1. Инверсионные связывающие функции различных моделей порядковой регрессии (взято из работы McCullagh и Nelder, 1983). Здесь, N-1 обозначает инверсионную нормальную функцию.
| Модель | Инверсионная связывающая функция Pε-1(Δ) | Плотность dPε(η)/dη |
| Логит | ||
| Пробит | ||
| Дополнительная модель повторного логарифма |
Для того чтобы оценить w и θ из нашей модели, для наблюдения (xi, y) мы можем видеть, что
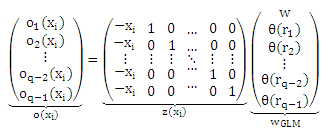
где oj(xi) = Pε-1 Pr(y ≤ rj|xi) является преобразованной вероятностью рангов, меньших или равных rj, заданных xi, который будет оцениваться из выборки преобразованными частотами данного события. Обратите внимание, что сложность модели определяется предположением о линейности (5) и Pε-1, которые можно рассматривать как регуляризатор в конечном уравнении правдоподобия. Для полного обучающего набора получаем
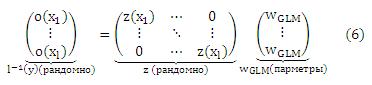
Последнее уравнение называется матрицей плана многомерной обобщенной линейной модели (GLM). Обобщенная линейная модель y = l(ZWGLM) в основном определяется матрицей плана Ζ и связывающей функцией l(⋅) = Pε (⋅). Тогда существуют заданный образец (X, Y), связывающая функция, которая совпадает с предположением о характере распределения данных, и методы расчета максимального правдоподобия WGLM (см. для подробностей McCullagh и Nelder [1983] или Fahrmeir и Tutz [1994]). Основная трудность в максимизации правдоподобия состоит в нелинейной связывающей функции.
В заключение этого обзора классических статистических методов мы хотели бы выделить два основных предположения для порядкового регрессии: (i) предположение стохастической упорядоченности пространства X (ii) и предположение о характере распределения ненаблюдаемой скрытой переменной.
Вместо предположений о характере распределения, рассмотренных в предыдущем разделе, рассмотрим параметризованное пространство отображений модели G от объектов к рангам. Каждая такая функция g порождает упорядочение >х по элементам пространства входа соответственно следующего правила
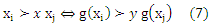
Если пренебречь упорядочением пространства Y, байесовская оптимальная функция g*class, как известно, минимизируется
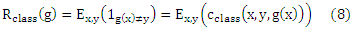
Перепишем Rclass(g) как
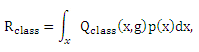
где
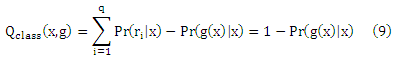
Более внимательное изучение уравнения (9) показывает, что достаточным условием для того, чтобы два отображения g 1 и g2 имели равные риски Rclass(g1) и Rclass(g2), является заданный Pr(g1 (x)|x= Pr(g2 (x)|x для любого х. Предполагая, что Pr(ri|x) является одинаковым для каждого х на определенном ряде rk, риски равны независимо от того, как «далеко» (относительно ранговой разницы) отображения g1(x) и g2(x) находятся от оптимального ранга argmaxri∈YPr(ri|x). Это наглядно показывает то, что cclass не подходит для случая, когда естественный порядок определяется на элементах Y.
Поскольку единственная доступная информация о рангах — это индуцированное упорядочение пространства входа X (уравнение (7)), мы утверждаем, что распределение независимой модели порядковой регрессии должно выделить функцию g*pref, которая вызывает упорядочение пространства X, что имеет наименьшее количество инверсий на парах (x1,x2) объектов (см. Sobel,1993). Чтобы смоделировать это свойство, необходимо отметить, что в связи с упорядочением пространства Y, каждое отображение g вызывает упорядочение пространства X по уравнению (7). Определим ранговую разницу ранга θ: YxY-> Ζ по
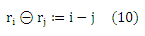
Теперь мы различаем заданную пару (x1, y1) и (x2, y2) объектов между двумя различными событиями: y1θy2 > 0 и y1θy2< 0. Согласно уравнению (7) функция g нарушает порядок, если y1θy2> 0 и g(x1)θg(x2) ≤ 0, или y1θy2< 0 и g(x1)θg(x2) ≥ 0. Кроме того, учитывая, что каждый слабый порядок >y порождает эквивалентность ~у [Fishburn, 1985] и автоматически создается случай y1θy2 =0. Таким образом, соответствующая функция потерь задается как
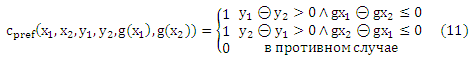
Обратите внимание, что мы можем получить m2 выборки в соответствии с p(x1, x2, y1, y2). Важно, чтобы эти выборки не являлись m2 iid выборками функции cpref(x1, x2, y1, y2, g(x1), g(x2)) для любой g. Кроме того, если мы определим
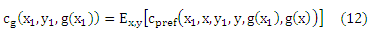
Минимизация функционального риска задается как
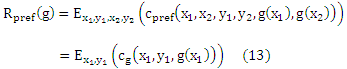
Хотя уравнение (13) указывает на большое сходство с классификацией функционального риска обучения (8), мы видим, что в связи с функцией потерь cg, которая использует порядковый характер Y, у нас имеется другая точечная функция потерь для каждого g. Таким образом, мы нашли функциональный риск, который может использоваться для порядковой регрессии и учитывает порядок в соответствии с предложением McCullagh и Nelder [1983].
Для того чтобы сопоставить Rpref(g) с простейшей классификацией риска мы повторно определим эмпирический риск, основываясь на данных обучения (X, Y). Для обозначений упрощения определим пространство ε событий пар х и у с неравными рангами по
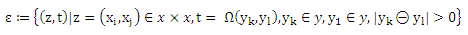
Кроме того, сокращенные обозначения x(1) и x(2) для обозначения первого и второго объекта пары нового набора обучения (X’, Y’) можно получить из (X, Y), если мы используем все 2 -множества в ε, выводимые из (X, Y), т. е.
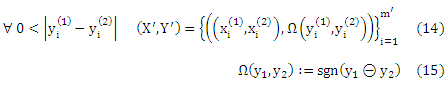
Где Ω является индикаторной функцией для ранговых разностей и m’ является кардинальным числом (X’,Y’).
Предположим, что задана неизвестная вероятностная мера p(x,y) на ΧxY. Тогда для каждого g: Χ→ Y верны следующие равенства
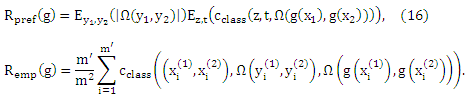
Доказательство. Выведем вероятность p(z,t) на ε, полученным из p(x1, x2, y1, y2):
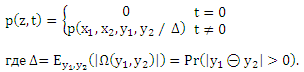
Используя формулировку (11) cpref мы убеждаемся, что
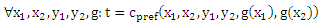
Первое утверждение доказано. Следующее утверждение следует из постановки Χ = X, Υ = Y и присвоения постоянной массы 1/m2 каждой точке (x1, x2, y1, y2). Учитывая, что каждая функция g ∈ G определяет функцию pg: Χ x Χ →{-1,0,+1} по
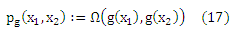
Теорема 1 утверждает, что эмпирический риск определенного отображения g на выборке (X, Y) эквивалентно cclass потере связанного отображения pg на выборке (Χ’,Υ’) с точностью до постоянного множителя m’/m2, который не зависит ни от g, ни от pg. Таким образом, проблему распределения независимой порядковой регрессии можно свести к задаче классификации пар объектов. Важно подчеркнуть ход суждений, которые приводят к этой эквивалентности. Исходная задача состояла в том, чтобы найти функцию g, которая отображает объекты в рангах, что заданы выборкой (X, Y). Принимая во внимание порядковый характер рангов, мы пришли к эквивалентной формулировке искомой функции pg, которая отображает пары объектов трех классов >y, <y и ~y. Возвращаясь к нашему ходу суждений, можно столкнуться с тем, что только те pg допустимы (в том смысле, что существует функция g, которая соответствует уравнению (17)), которые определяют асимметричное и транзитивное отношение к X. Поэтому мы и называем это проблемой предпочитаемого обучения. Баесовая оптимальная решающая функция может привести к функции pg, которая уже не транзитивна к X (Herbrich и соавт., 1998). Что также известно как проблема стохастической транзитивности (Suppes и соавт., 1989). Отметим также, что условия транзитивности и асимметрии эффективно уменьшают пространство допустимых функций классификации pg, оказывающих влияние на пары объектов.
Тем не менее, приведенная выше формулировка (в представленной форме) не подходит для непосредственного применения классических результатов теории обучения. Причина состоит в том, что построенные выборки пар объектов нарушают iid предположение. Для того чтобы по-прежнему смочь ограничить риск для предпочитаемого обучения, мы должны снизить нашу выборку таким образом, чтобы конечная реализация потерь (11) распространялась на iid. При этом условии можно ограничить отклонение ожидаемого риска от эмпирического риска. Пусть σ будет любой перестановкой чисел 1, …,m. Кроме того, для удобства записи пусть Cg(i,j) сокращает обозначение cpref(xi, xj, yi, yj, g(xi), g(xj)). Тогда можно увидеть, что для любых g ∈ G
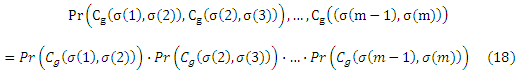
Очевидно, m — 1 является максимальным количеством пар объектов, которые все еще удовлетворяют iid предположение. Для того, чтобы убедиться в этом, учтем, что в силу своей транзитивности упорядочение g(x1)<y g(x2) и g(x2)<y g(x3) подразумевает g(x1)<y g(x3) (и, наоборот, для >у и ~у). Теперь мы можем привести следующую теорему.
Пусть p будет вероятностной мерой на Χ x {r1,… ,rq}, пусть (X, Y) будет выборкой величины m iid, извлеченной из p. Пусть σ будет какой-либо перестановкой чисел 1,…, m. Для каждой функции g: X → {r1,… ,rq} существует функция f ∈ F и вектор θ, так что (обратите внимание на тесную связь с кумулятивной моделью):
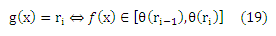
Пусть fat — размерность множества функций F, ограничена функцией afatF: R → N. Тогда для каждой функции g с нулевой ошибкой обучения, т.е.
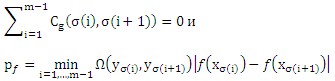
С вероятностью 1-δ
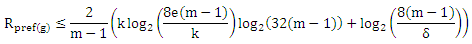
где k = afatF(pf/8) ≤ e(m — 1).
Рассмотрим действительную функцию классификации F, имея fat-функцию, ограниченную функцией afatF: R → N (как указано выше), которая является непрерывной справа. Зададим θ ∈ R. Тогда с вероятностью 1 — δ обучающийся, который правильно классифицирует m iid выборки (x1,y1),…, (xm,ym) с таким h = Tθ(f)∈Tθ(F), что h(xi) = yi, i=1,…, m и pf=mini yi(|f(xi)— θ|), будут иметь погрешность h, ограниченную по
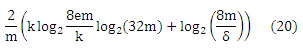
где k = afatF(pf/8) ≤ em.
Учитывая, что по построению мы получили m — 1 iid выборки и что классификация пары осуществляется по решению, основанном на разности f(x(σi)) — f(x(σi+1)), мы можем повысить границу Rpref(g), путем замены каждой m на m — 1 и используя θ = 0.
afatF(p) раздробленную размерность F можно рассматривать как максимальное число объектов, которые можно расположить в любом порядке с помощью функций из F и минимальным отступом min Ω(y1, y2)|f(x1)-f(x2)| для р (используя уравнение (7) вместе с (19)). Отметим, что условие нулевой ошибки обучения для вышеуказанного ограничения автоматически удовлетворяет любую σ, если Remp(g) = 0. Даже если этот эмпирический риск не был основан на iid выборке, его минимизация позволяет применять вышеуказанное ограничение. В следующем разделе мы представим алгоритм, который направлен на минимизацию именно этого эмпирического риска, единовременно осуществляя отступ границы ранга.
На основании результатов теоремы 2 мы предлагаем моделировать ряды как интервалы оси. Как и в классической кумулятивной модели, что используется в порядковой регрессии, введем для каждой функции g (скрытую) линейную функцию f : X → R
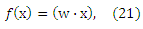
которая связана с уравнением (19). Для того чтобы применить данную теорему, нам необходимо найти функцию f*, которая не приводит к ошибке обучения на (Χ’,Υ’), контролируя при этом обобщенную ошибку путем максимизации ограничения pf. Заметим, что
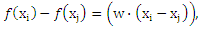
что делает очевидным то, что каждая пара (xi, xj) ∈ X’ представлена разностью векторов (xi — xj), предполагающей линейную модель f. Это позволяет напрямую применять алгоритм большого отступа с заменой каждого xi на (xi(1)-xi(2)). Таким образом, максимизация отступа происходит на границах ранга θ(ri) (см. уравнение (19) и рис 1).
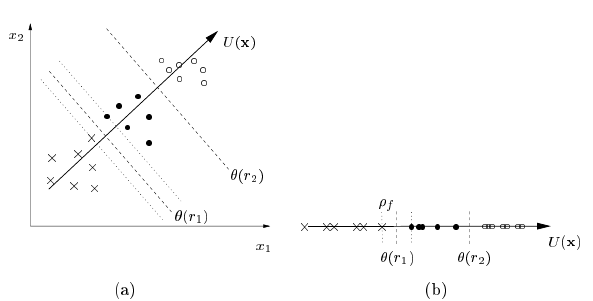
Рисунок 1. (a) Отображение объектов из ранга r1 (x), ранга r2 (•) и ранга r3 (o) к осям координат f(x), где x = (x1, x2)T. Стоит отметить, что по θ (r1) и θ (r2) определяются две связанные гиперплоскости. (b) Отступ связанных гиперплоскостей pf = min(Χ’,Υ’) Ω(yi(1), yi(2))|f(xi(1))-f(xi(2))| задается временем на границах ранга θ(ri).
На практике предпочтительно использовать алгоритм большого отступа для разложения с мягким отступом. Кроме того из-за условия Каруша—Куна—Таккера w* можно записать согласно данных обучения. Что дает
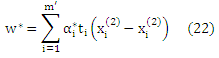
где α* задано
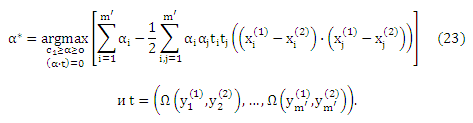
Однако следует отметить, что в связи с разложением последнего члена в (23),
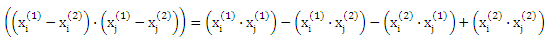
решение α* для этой проблемы можно вычислить исключительно с точки зрения внутреннему скалярному произведению векторов признаков, не ссылаясь на сами вектора признаков. Таким образом, можно успешно применять идею (неявного) отображения данных X через нелинейное отображение Φ: Χ -> F в пространстве признаков F. Замена каждого появления х на Φ(х) дает
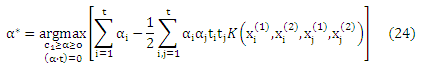
где K для данной функции k определяется по
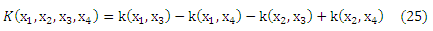
Здесь k : Χ x X → R является ядром Мерсера и для постоянных отображений Φ определяется по
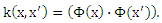
Обратите внимание, что использование ядер вместо явного употребления отображений Φ позволяет нам иметь дело с нелинейными функциями f, не сталкиваясь с вычислительными трудностями. Кроме того, как указано в теореме 2 ограничение риска Rpref(w) не зависит от размерности F, но зависит от отступа ρf.
Для того чтобы оценить границы ранга отметим, что разница в f* больше или равна единице для всех обучающих выборок, которые представляют собой правильно классифицированную пару. Этого легко можно добиться путем проверки 0 < αi* < C, то есть, обучающего образа, который не соответствуют полю ограничения. Таким образом, если θ(k) ⊂ X’ является долей объектов обучающей выборки с 0 < αi* < C и ранговой разницей θ, начиная с ранга rk,, то есть,
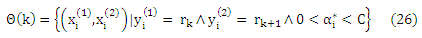
то оценка θ(rk) задается
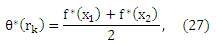
Где
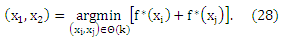
Другими словами, оптимальный порог θ*(rk) для ранга rk лежит посередине ближайших утилит (в смысле их полезности) объектов рангов rk и rk+1. После оценки границ ранга θ(rk), ему присваивается новый объект в соответствии с уравнением (19).
Мы хотим подчеркнуть, что используя разность векторов вместо пары объектов, можно эффективно объединить все гиперплоскости f(x) = θ(rk), таким образом, это приведет к стандартной задаче квадратичного программирования. Кроме того, эффективное объединение сохраняется, если мы используем общие lq-отступы. Это делает представленный алгоритм подходящим для выполнения задачи порядковой регрессии. Стоит отметить, что ядро K также получено из k действий, совершенных исключительно в F и, таким образом не учитывает слишком большого гипотетического пространства. Все свойства являются следствиями моделирования рангов как интервалов на оси и предварительного знания упорядочения Y.
В этом разделе мы представим некоторые опытнее данные для алгоритма, представленного в предыдущем разделе. Начнем с того, что зададим результаты для моделированных данных, что позволит нам анализировать наш алгоритм в контролируемых условиях. Затем зададим кривые обучения для примера из области информационного поиска.
В этом эксперименте мы хотим сравнить обобщенное поведение нашего алгоритма с multi-class SVM [Weston и Watkins, 1998] и регрессией опорных векторов (SVR) (ср. Smola, 1998) — предпочтительные методы, если не учитывать порядковую природу Y, а вместо этого рассматривать ранги как классы (классификация) или непрерывные значения отклика (оценка регрессии). Еще одной причиной для выбора этих алгоритмов является сходство их регуляризатора ‖w‖2 и гипотетического пространства F, что делает их максимально сопоставимыми. Мы получили 1000 наблюдений x = (x1,x2) в единичном квадрате [0,1]x[0,1] ⊂ R2 в соответствии с равномерным распределением. Мы присваиваем каждому наблюдению x значение у в соответствии с
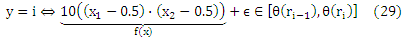
где ε было нормально распределенным, т.е. ε ~ N(0, 0.125), а θ = (—∞,—1, —0.1, 0.25, 1, +∞) является вектором предопределенного порога. На рисунке 2 (а) показаны точки xi, которые относятся к разным рангам, после добавления величины εi, которая распределена по нормальному закону. Если рассматривать всю задачу в качестве задачи классификации, то мы бы назвали их неправильно классифицированными примерами обучения. Сплошные линии на рисунке 2 (а) показывают «истинные» границы ранга θ на f(x).
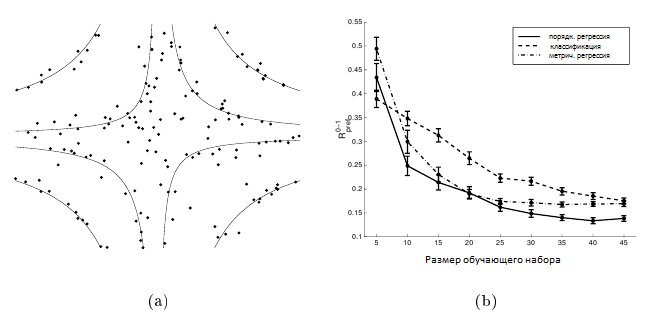
Рисунок 2. (а) график рассеяния точек х, f(x) которых сопоставляется с другими интервалами, чем f(x)+ε (см. уравнение (29)). (б) кривые обучения для multi-class SVM (пунктирные линии), регрессии опорных векторов (штрихпунктирная линия) и алгоритма порядковой регрессии (сплошная линия) при измерении Rpref. Планки погрешностей отображают 95% интервала доверия расчетного риска Rpref.
Для сравнения трех различных алгоритмов мы произвольно отобрали 100 обучающих выборок (X,Y) из обучающего набора размером m от 5 до 45, тем самым убедившись, чтобы, по крайней мере, один представитель каждого ранга был в пределах выбранного обучающего набора. Классификацию с multi-class SVM проводили путем попарного вычисления 5 • 4/2 = 10 гиперплоскостей. Для всех алгоритмов, представленных в предыдущем разделе, мы выбрали ядро k(xi,xj) = ((xi•xj)+1)2 и компромиссный параметр C = 1000000. В частном случае регрессии опорных векторов мы использовали значение ε = 0,5 для ε-независимой функции потерь (см. [Vapnik, 1995] для определения этой функции потерь) и пороги θ = (0.5, 1.5, 2.5, 3.5, 4.5) для преобразования вещественных прогнозов в ранги.
Для того чтобы оценить риск Rpref(g*)/Ey1,y2(|Ω(y1,y2)|) остальных 955-995 точек, мы усреднили все 100 результатов обучающего набора заданного размера. Таким образом, мы получили три кривых обучения, показанные на рисунке 2 (б). Обратите внимание, что мы использовали масштабированный Rpref — который больше чем постоянный коэффициент. Видно, что алгоритм, предложенный для порядковой регрессии, обобщает намного быстрее по сравнению с классификацией, если использовать порядковый характер Y. Это можно объяснить тем, что модель скрытой полезности связывает все «гиперплоскости» f(x) = θ(rk)(см. рис.1), что не относится к случаю с multi-class SVM. Кроме того, кривые обучения для SVR и предложенного алгоритма порядковой регрессии очень близки. Это можно объяснить тем, что заранее заданные пороги θ(rk) определены таким образом, что их попарное различие составляет около 0,5 — размер заранее выбранной ε — трубы. Поэтому, полезность и непрерывные ранги, оцененные алгоритмом регрессии, являются величиной одного порядка, что приводит к таким же обобщенным поведениям.
На рисунке 3 мы отразили распределение единичного квадрата по рангам r1 (черные области) и рангам r5 (белое поле) для функции обучения g*(x), полученной из случайных обучающих наборов, начиная от размера m = 5 (верхний ряд) до m = 25 (нижний ряд). Мы использовали те же параметры, что и для расчета кривых обучения. В крайней правой колонке (e) показано верное распределение, т. е. y=ri <-> f(x) ∈ [θ(ri-1, θ(ri))]. В первой колонке (а) мы можем видеть, как работает алгоритм, представленный в предыдущем разделе, с обучаемым набором различных размеров. Как и ожидалось, для обучающего набора размером m = 25 алгоритм построил функцию полезности вместе с набором порогов, что очень хорошо представляет правильное ранжирование. Во второй колонке (b) показаны результаты вышеуказанного multi-class SVM при выполнении задачи. Здесь парные гиперплоскости не связаны, так как не учитывается порядковый характер Y. Это приводит к худшему обобщению, особенно в областях, где не заданы точки обучения. В третьей колонке (с) показано распределение, проделанное с помощью алгоритма SVR, если представить каждый ранг ri как i. Кривая обучения дает хорошие результаты, поэтому обобщенное поведение сравнимо с методом порядковой регрессии (первая колонка). Недостаток SVR для решения этой задачи становится очевидным, когда мы изменяем представление рангов. В четвертой колонке (d) мы применили тот же алгоритм SVR, на этот раз представив exp(i) вместо ранга ri. Как видно, это резко изменяет обобщенное поведение метода SVR. Мы пришли к выводу, что важнейшей задачей для применения метрических методов оценки регрессии к задаче порядковой регрессии является определение представления о рангах. Это автоматически, хотя и более трудоемко, решается с помощью предложенного алгоритма.
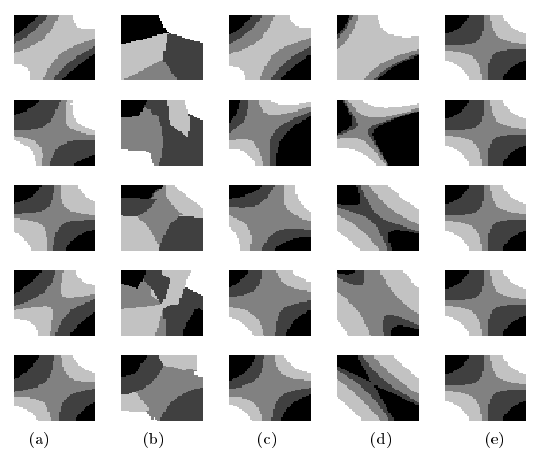
Рисунок 3. Распределение точек по рангам r1 (черные области) и рангам r5 (белое поле) для функции обучения g*(x), основанной на случайно выбранных обучающих выборках размером 5, 10, 15, 20 и 25 (от верхнего до нижнего ряда), (а) Результаты алгоритма, представленного в предыдущем разделе. (b) Результаты multi-class SVM, когда мы рассматриваем каждый ранг как класс, (с) Результаты SVR если мы представим ранг ri как i. (d) Результаты SVR, если мы представим ранг ri как вещественное число exp(i). (е) Основное распределение, не учитывающее помех.
В этом эксперименте мы выдвинули следующее предположение: после первоначального (текстового) запроса пользователь переходит к информационно-поисковой системе (ИПС), которая возвращает набор документов пользователю. Теперь пользователь присваивает ранги к небольшой доле возвращенных документов, а задача алгоритма обучения заключается в том, чтобы присвоить ранги оставшимся неотранжированным документам для их ранжирования. Мы предполагаем, что величина интереса представляется процентом инверсий, вносимых ранжированием при помощи алгоритма обучения. Эта величина попала в Remp(g)/m’ (m’ = |(X’,Y’)|(см. уравнение 14 для точного определения) и, таким образом, после использования m = 6 до m = 24 документов и их соответствующего ранжирования, мы измеряем это значение для остальных документов. Для этого эксперимента были использованы те же параметры, что и в предыдущем эксперименте. Для исследования был выбран набор данных OHSUMED, собранный Уильямом Хершом , который состоит из 348 566 документов и 106 запросов с соответствующими ранжированными результатами. Рассматривают три ранга: «соответствующий (релевантный) документ», «частично релевантный документ» и «нерелевантный документ» относительно заданного текстового запроса. Для наших экспериментов мы использовали результаты запроса № 1 («Возможно ли продвижение сайтов в органическом поиске без ссылок вообще?»), который состоит из 107 документов, выбранных из полной базы данных. Для того чтобы применить наш алгоритм мы использовали распределение набора слов [Salton, 1968], то есть, мы для каждого документа вычислили вектор компонентов меры TF-IDF: «частота слова/обратная частота документа». TFIDF является мерой взвешивания набора слов, которая дает более высокий вес тем словам, которые очень редко встречаются по всем документам. Мы ограничились термами, которые, по крайней мере, трижды появляются во всей базе данных. Это приводит к ≈ 1700 термам, которые приводят к определенному документу очень высокой размерности, но разряженному вектору. Мы нормировали длину каждого вектора документа к единице (см. Joachims [1998]).
На рисунке 4 (а) показаны кривые обучения для multi-class SVM и нашего алгоритма для порядкового регрессии, выраженные относительно количества вносимых инверсий. Как видно из графика, предложенный алгоритм имеет достаточно хорошее обобщенное поведение по сравнению с алгоритмом, который рассматривает каждый ранг в качестве отдельного класса. На рисунке 4 (б) показаны кривые обучения для обоих алгоритмов, если мы измеряем количество неправильной классификации – рассматриваем ранги в качестве классов. Как и ожидалось, multi-class SVM работает намного лучше, чем наш алгоритм. Важно отметить, опять же, что сведение к минимуму нуль-единичной потери Rclass не приводит автоматически к минимальному числу инверсий и, следовательно, к оптимальному упорядочению.
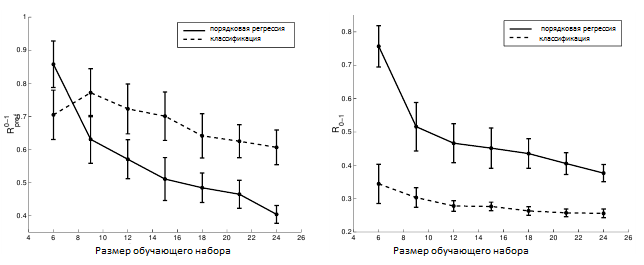
Рисунок 4. Кривые обучения для multi-class SVM (пунктирная линия) и алгоритма порядковой регрессии (сплошная линия) для запроса № 1 по набору данных OHSUMED, когда мы измеряем (а) Rpref и (б) Rclass. Планки погрешностей отображают 95% интервалов доверия.
На рисунке 5 (а) показаны кривые обучения для SVR и нашего алгоритма порядковой регрессии, выраженные относительно количества вносимых инверсий. Алгоритм SVR достаточно хорошо показал себя на искусственном наборе данных, но на реальном наборе данных он не смог подобрать ранжирование, которое бы минимизировало число инверсий. Это можно объяснить тем, что для реального примера равноудаленность в предполагаемой утилите больше не может удерживаться — особенно принимая во внимание то, что область данных довольно разряженная для такого рода проблемы. Аналогично на рисунке 5 (б) показаны кривые обучения для обоих алгоритмов, если мы измеряем количество неправильной классификации. Как и следовало ожидать, правые кривые алгоритма SVR показывают худшие результаты даже при таком измерении. Обратите внимание, что алгоритм SVR минимизирует ни Rpref, ни R0-1, которые могут объяснить его плохое обобщенное поведение. Также обратите внимание на то, что мы не адаптируем параметр ε — размер трубки. Причина состоит в том, что в этой конкретной задаче не было бы достаточного количества примеров обучения, способных оставить обоснованную их часть для проверки.
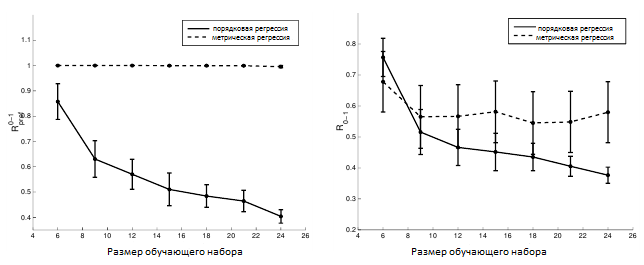
Рисунок 5. Кривые обучения для SVR (пунктирная линия) и алгоритм порядковой регрессии (сплошная линия) для запроса № 1 по набору данных OHSUMED, когда мы измеряем (а) Rpref и (б) Rclass. Планки погрешностей отображают 95% интервалов доверия.
Сейчас мы рассмотрели задачу порядкового регрессии, которая в основном характеризуется порядковым характером пространства исходов Y. Все известные подходы к данной проблеме представляют предположения о характере расположения базисной непрерывной случайной величины. В отличие от этого, мы предложили функцию потерь, которая позволяет, применяя независимые методы распределения, решать задачи порядковой регрессии. Используя тот факт, что введенная классифицирующая функция потерь представляет собой набор индикаторных функций, мы могли бы создать независимое распределительное ограничение предложенного нами риска. Кроме того, мы смогли показать, что для каждой задачи порядковой регрессии существует соответствующая задача предпочтительного обучения на парах объектов. В результате этого создается связь между порядковой регрессией и методами классификации — на этот раз действительно на парах объектов. Для представления рангов на промежутках оси, мы могли бы задать ограничения отступа предложенного нами риска — на этот раз действительно на границах ранга. На основании этого результата мы представили алгоритм, который подобен известному алгоритму опорных векторов, но более эффективно связывает гиперплоскости, которые используются для определения ранга.
Стоит отметить, что представленная нами потеря включает пары объектов, и как мы можем увидеть, проблему multi-class классификации также можно переформулировать на пары объектов, что приведет к проблеме обучения отношения эквивалентности. Обычно, для того чтобы расширить метод двоичной классификации для многосторонних классов, разрабатываются методы один-против-одного или один-против-всех [Hastie и Tibshirani, 1998, Weston и Watkins, 1998]. Такие методы увеличивают размер гипотетического пространства квадратично или линейно числу классов, соответственно. Последние работы [Phillips, 1999] показали, что обучение отношения эквивалентности может увеличить обобщенное поведение методов двоичного класса, если расширить его до многосторонних классов.
Оригинал: «Large Margin Rank Boundaries for Ordinal Regression»
Обучение ранжированию I. Попарный подход. Часть 2: Введение в RankBoost
Обучение ранжированию I. Попарный подход. Часть 3: Экспериментальная оценка RankBoost
Полезная информация по продвижению сайтов:
Перейти ко всей информации